当前位置:网站首页>PTA search tree judgment
PTA search tree judgment
2022-07-22 18:50:00 【Canned】
4-2- Binary search tree Search tree judgment (25 branch )
For binary search trees , We stipulate that the left subtree of any node contains only the key values which are strictly smaller than the node , And its right subtree contains the key value greater than or equal to the node . If we swap the left and right subtrees of each node , The resulting tree is called a mirror binary search tree .
Now let's give a sequence of integer key values , Please write a program to judge whether the sequence is a preorder traversal sequence of a binary search tree or a mirror binary search tree , If it is , Then output the post order traversal sequence of the corresponding binary tree .
Input format :
The first line of input contains a positive integer N(≤1000), The second line contains N It's an integer , For the given sequence of integer key values , Numbers are separated by spaces .
Output format :
The first line of the output first gives the judgment result , If the input sequence is the preorder traversal sequence of a binary search tree or a mirror binary search tree , The output YES, No side output NO. If it turns out that YES, The next line outputs the post order traversal sequence of the corresponding binary tree . Numbers are separated by spaces , But there can't be extra spaces at the end of the line .
sample input 1:
7
8 6 5 7 10 8 11
sample output 1:
YES
5 7 6 8 11 10 8
sample input 2:
7
8 6 8 5 10 9 11
sample output 2:
NO
The main idea is
1. Generate binary search tree ( The preorder traversal of a binary search tree must be equal , Therefore, it can be used to judge whether it belongs to the preorder traversal of a search tree )( We have been struggling with different sequences before, but the search trees built with the same number are not necessarily the same )
2. Judge whether the preorder traversal of the search tree is the same as that given
#include<stdio.h>
#include<stdlib.h>
#define max 10000
int a[max], b[max],c[max];
int t;// Global variables are also very useful
typedef struct node* Tree;
struct node {
int data;
Tree Left;
Tree Right;
};
Tree Insert(Tree T, int x)
{
if (T == NULL) {
// Recursive export , In recursive programs, I think this is actually the hardest thing to think of
T= (Tree)malloc(sizeof(struct node));
T->data = x;
T->Left = T->Right = NULL;
}
else {
if (x <T->data) {
T->Left = Insert(T->Left, x);
}
else {
T->Right = Insert(T->Right, x);
}
}
return T;
}
Tree swap(Tree T)
{
if (T) {
// If you use T->Left&&T->Right, Then when one is empty and the other is not empty, there will be segment errors , Exchange from the lower layer
T->Left = swap(T->Left);
T->Right = swap(T->Right);
Tree tmp;
tmp = T->Left;
T->Left = T->Right;
T->Right = tmp;
}
return T;
}
void pre(Tree T)// The first sequence traversal
{
if (T) {
b[t++] = T->data;
pre(T->Left);
pre(T->Right);
}
}
void post(Tree T)
{
if (T) {
post(T->Left);
post(T->Right);
c[t++] = T->data;
}
}
int main()
{
int n,flag=0,i;
Tree T = NULL,T1;
scanf("%d", &n);
for (int k = 0; k < n; k++) {
scanf("%d", &a[k]);
T=Insert(T, a[k]);
}
if (n == 1) {
printf("YES\n%d", a[0]);
return 0;
}
t = 0;// Every time you call pre perhaps post To initialize
pre(T);//b
for (i = 0; i < n; i++) {
if (a[i] != b[i]) {
flag++;
break;
}
}
if (flag == 0) {
t = 0;
post(T);
printf("YES\n");
for (i = 0; i < n; i++) {
if (i == 0)printf("%d", c[i]);
else printf(" %d", c[i]);
}
}
else {
t = 0;
T1=swap(T);
pre(T1);
for (i = 0; i < n; i++) {
if (a[i] != b[i]) {
flag++;
break;
}
}
if (flag == 1) {
t = 0;
post(T);
printf("YES\n");
for (i = 0; i < n; i++) {
if (i == 0)printf("%d", c[i]);
else printf(" %d", c[i]);
}
}
else
printf("NO");
}
return 0;
}
attach : Search trees built with different sequences but the same number are not necessarily the same
Description
Judge whether two sequences are the same binary search tree sequence
Input
Start a number n,(1<=n<=20) Express n One needs to be judged ,n= 0 The end of the input .
The next line is a sequence , The sequence length is less than 10, contain (0~9) The number of , No repetition of numbers , According to this sequence, a binary search tree can be constructed .
It follows that the n Yes n A sequence of , Each sequence has the same format as the first sequence , Please judge whether these two sequences can form the same binary search tree .
Output
If the sequence is the same, output YES, Otherwise output NO
Sample Input
6
45021
12045
54120
45021
45012
21054
50412
0
Sample Output
NO
NO
YES
NO
NO
NO
HINT
Source
边栏推荐
- Alibaba's previous SMS service is no longer available
- strncpy() 复制字符串(受长度限制)
- App mobile End test [6] application (APK) package Management and Activity
- How PHP prevents CSRF attacks
- Qt | 模態對話框和非模態對話框 QDialog
- Go 内存模型
- [audio] transplant wm8978 audio codec driver based on STM32 I2S
- 周末和技术大咖们聚餐,聊到了软件测试行业的“金九银十”高峰【内卷之势已然形成】
- Summary 20220210
- LeetCode: 627. 变更性别
猜你喜欢

05.迪米特原则(Law of Demeter LoD)

1.雷点:mysql数据库转移到oracle,2.qt5.12.3 连接oracle 12c数据库

Go 语言重要知识点:字符串、UTF-8 编码、rune

App移動端測試【6】應用程序(apk)包管理與activity

06. Liskov Substitution Principle (LSP)

Important knowledge points of go language: string, UTF-8 encoding, Rune

05. Law of Demeter LOD

strncpy() 复制字符串(受长度限制)
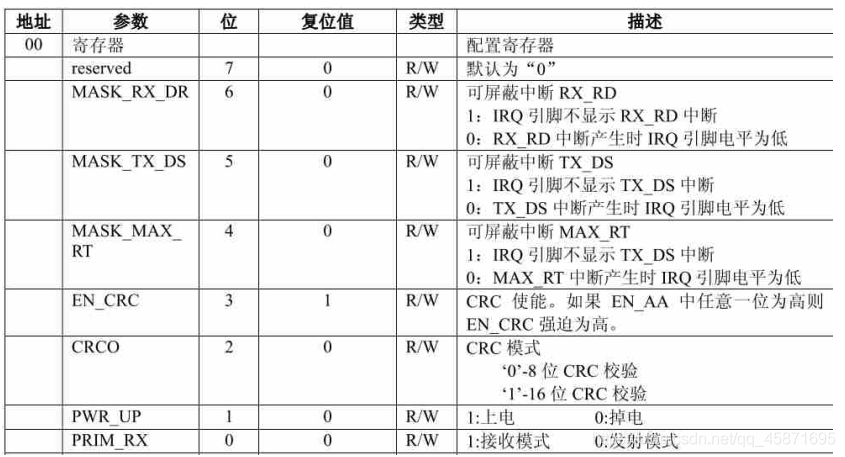
NRF24L01 wireless module setting transmit receive mode method

Uniapp wechat applet map, open in Gaode app, Tencent app, baidu app, apple map app
随机推荐
【FatFs】基于STM32 SD卡移植FatFs文件系统
总结20220209
Qt | boîtes de dialogue modales et non modales qdialog
总结20220211
05.迪米特原则(Law of Demeter LoD)
Go 语言学习:Go 语言之旅——练习题及参考答案
递归求简单交错幂级数的部分和 (15分)
LeetCode: 1179. 重新格式化部门表
Summary 20220211
周末和技术大咖们聚餐,聊到了软件测试行业的“金九银十”高峰【内卷之势已然形成】
Summary 20220119
02. Dependency Inversion Principle
[SDIO] sd2.0 protocol analysis summary (II) -- SD card identification & data transmission process
Codeforces Round #799 (Div. 4)(8/8)
How can ECSHOP run super slow locally?
AMH multiple MySQL versions coexist?
ps: 如何调出辅助线
Log4J日志配置详解
1.mysql null 和 in;2.127.0.0.2是啥?
【QT源代码复用】模拟QCompleter的弹窗方式