当前位置:网站首页>堆(优先级队列)
堆(优先级队列)
2022-07-22 00:45:00 【m0_60631323】
目录
一、优先级队列
1.1概念
在前面的学习中我们知道,队列是一种先进先出的数据结构,但在有些情况下,操作的数据可能带有优先级,此时使用队列是很难实现的
这种情况下,我们的数据结构应该提供最基本的两个操作,一个是返回最高优先级对象,一个是添加新的对象,这种数据结构就是优先级队列(Priority Queue)。.
二、优先级队列的模拟实现
JDK1.8中的PriorityQueue底层使用了堆的数据结构,而堆实际就是在完全二叉树的基础之上进行了一些元素的调整。
注意:
- 堆采用的完全二叉树结构,此时的树的节点按照顺序存储的方式存储在数组中.
- 区别于前面学习的二叉树的链式存储
2.1堆的概念
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大堆)。
堆的性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
2.2堆的存储方式
因为堆是一棵完全二叉树,故堆可以以层序遍历的方式顺序的存储在数组中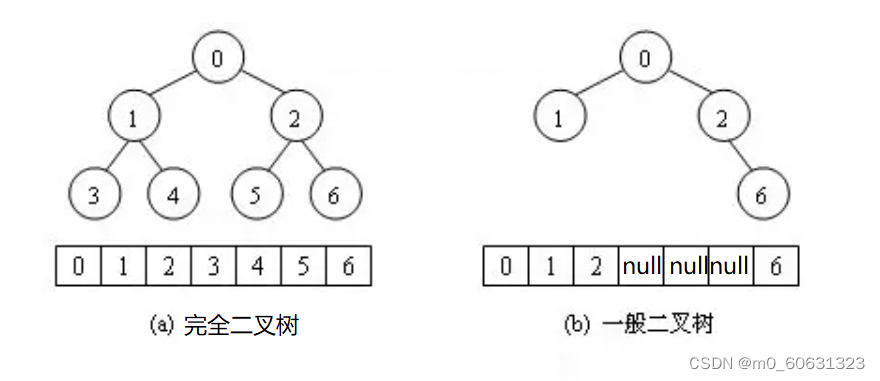
注意:
对于非完全二叉树,不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须存储空节点,导致空间利用率低
将节点存储到了数组中后,可以根据下面的二叉树的性质对二叉树进行还原,假设i为节点在数组中的下标:
- 如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2
- 如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
- 如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子
2.3堆的创建
对于集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据,如果将其创建成堆呢?
我们先以完全二叉树的形式还原这棵树
下面我们以创建一个大根堆为例
总结:
1.从最后一棵子树调整
最后一棵子树的根节点的下标为p=(arr.length-1-1)/2;
p–得到下一棵子树根节点的下标
2.每棵子树调整的时候,都是向下调整
3.每棵子树向下调整的结束位置都是arr.length-1;
代码:
public static void shiftDown(int parent) {
//child先标记parent的左孩子,因为parent可能有左孩子没有右孩子
int child = 2 * parent + 1;
while (child < size) {
//如果右孩子存在,找到左右孩子中较大的孩子,用child进行标记
if(child+1 < size && array[child+1] >array[child]){
child += 1;
}
//如果双亲比其最小的孩子还大,说明该结构已经满足堆的特性了
if (array[parent] >= array[child]) {
break;
}else{
//将双亲与较大的孩子交换
int t = array[parent];
array[parent] = array[child];
array[child] = t;
//parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整
parent = child;
child = parent * 2 + 1;
}
}
}
public static void createHeap(int[] array) {
// 找倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,遇到一个节点,应用向下调整
int root = ((array.length-2)>>1);
for (; root >= 0; root--) {
shiftDown(root);
}
}
向下调整(shiftDown)的时间复杂度:
最坏情况就是调整树的高度次,即O(logN);
建堆的时间复杂度分析:
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果)
故建堆的时间是复杂度为O(N)
2.4堆的插入和删除
2.4.1 堆的插入
堆的插入共分为两个步骤:
1.将元素插入到堆的末尾,也就是最后一个孩子之后(如果空间不够需要扩容)
2.将最后插入的节点向上调整,直到满足堆的性质
下面演示的是在一个小根堆上插入元素的过程

代码:
public void offer(int e){
array[size++]=e;
shiftUp(size-1);
}
public void shiftUp(int child) {
//找到child的双亲
int parent = (child - 1) / 2;
while (child > 0) {
//如果双亲比孩子小,parent满足堆的性质,调整结束
if (array[parent] < array[child]) {
break;
}
else{
//将双亲与孩子节点进行交换
int t = array[parent];
array[parent] = array[child];
array[child] = t;
// 小的元素向下移动,可能到值子树不满足对的性质,因此需要继续向上调增
child = parent;
parent = (child - 1) / 2;
}
}
}
堆的插入的时间复杂度:O(logN)
2.4.2堆的删除
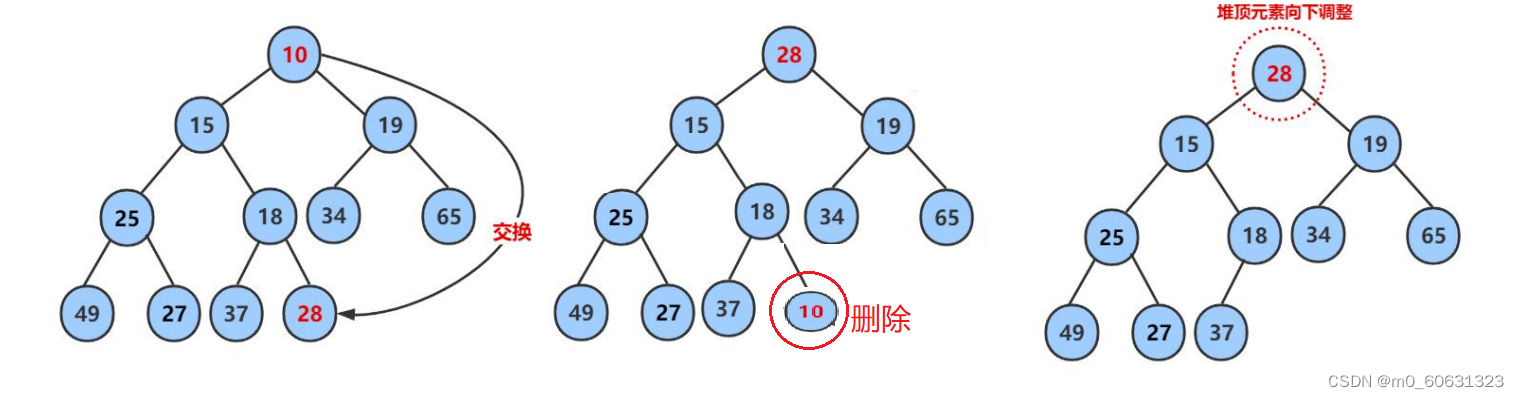
堆的删除一定删除的是堆顶元素
具体步骤如下:
具体如下:
- 将堆顶元素对堆中最后一个元素交换
- 将堆中有效数据个数减少一个
- 对堆顶元素进行向下调整
public int poll(){
int oldValue=array[0];
array[0]=array[--size];
shiftDown(0);
return oldValue;
}
2.4.3堆模拟实现优先级i队列
public class MyPriorityQueue {
private int[] array = new int[100];
private int size = 0;
public void offer(int e){
array[size++]=e;
shiftUp(size-1);
}
public int peek(){
return array[0];
}
public int poll(){
int oldValue=array[0];
array[0]=array[--size];
shiftDown(0);
return oldValue;
}
public void shiftDown(int parent) {
//child先标记parent的左孩子,因为parent可能有左孩子没有右孩子
int child = 2 * parent + 1;
while (child < size) {
//如果右孩子存在,找到左右孩子中较大的孩子,用child进行标记
if(child+1 < size && array[child+1] >array[child]){
child += 1;
}
//如果双亲比其最小的孩子还大,说明该结构已经满足堆的特性了
if (array[parent] >= array[child]) {
break;
}else{
//将双亲与较大的孩子交换
int t = array[parent];
array[parent] = array[child];
array[child] = t;
//parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整
parent = child;
child = parent * 2 + 1;
}
}
}
public void shiftUp(int child) {
//找到child的双亲
int parent = (child - 1) / 2;
while (child > 0) {
//如果双亲比孩子小,parent满足堆的性质,调整结束
if (array[parent] < array[child]) {
break;
}
else{
//将双亲与孩子节点进行交换
int t = array[parent];
array[parent] = array[child];
array[child] = t;
// 小的元素向下移动,可能到值子树不满足对的性质,因此需要继续向上调增
child = parent;
parent = (child - 1) / 2;
}
}
}
}
2.5常见习题


2.

3.

4.

三、PriorityQueue介绍
3.1PriorityQueue的特性
Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的,这里主要介绍PriorityQueue。
使用PriorityQueue的注意事项:
- 使用时必须导入PriorityQueue所在的包,即:
import java.util.PriorityQueue;
- PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出
ClassCastException异常 - 不能插入null对象,否则会抛出NullPointerException
- 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
- 插入和删除元素的时间复杂度为O(logN)
- PriorityQueue底层使用了堆数据结构
- PriorityQueue默认情况下是小堆—即每次获取到的元素都是最小的元素
如果需要使用大堆需要用户提供比较器 - PriorityQueue的默认容量是11 :

3.2 PriorityQueue的常用接口
PriorityQueue中的重要属性
- 构造方法
所有的构造方法
下面主要介绍几种常见的构造方法
(1) 不带参数的构造方法
发现不带参数的构造方法会调用带两个参数的构造方法,并指定容量为默认初始容量11
(2) 带一个参数的构造方法
(3)带两个参数的构造方法
(4)利用集合创建优先级队列
使用示例:
public static void main(String[] args) {
ArrayList<Integer> list = new ArrayList<>();
list.add(4);
list.add(3);
list.add(2);
list.add(1);
//用ArrayList对象来构造一个优先级队列的对象
PriorityQueue<Integer> q3 = new PriorityQueue<>(list);
System.out.println(q3.size());//4
System.out.println(q3.peek());//1
}
- 插入/删除/获取优先级最高的元素 功能介绍以及源码分析

(1)插入元素的过程
第一次插入元素的过程

第二次插入元素的过程:
建一个大根堆
public static void main(String[] args) {
PriorityQueue<Integer> q=new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});
q.offer(10);
q.offer(20);
q.offer(30);
System.out.println(q.peek());//30
}
JDK1.8中的扩容方式
3.3 优先级队列的应用
TOP-K问题:即求数据集合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆 - 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。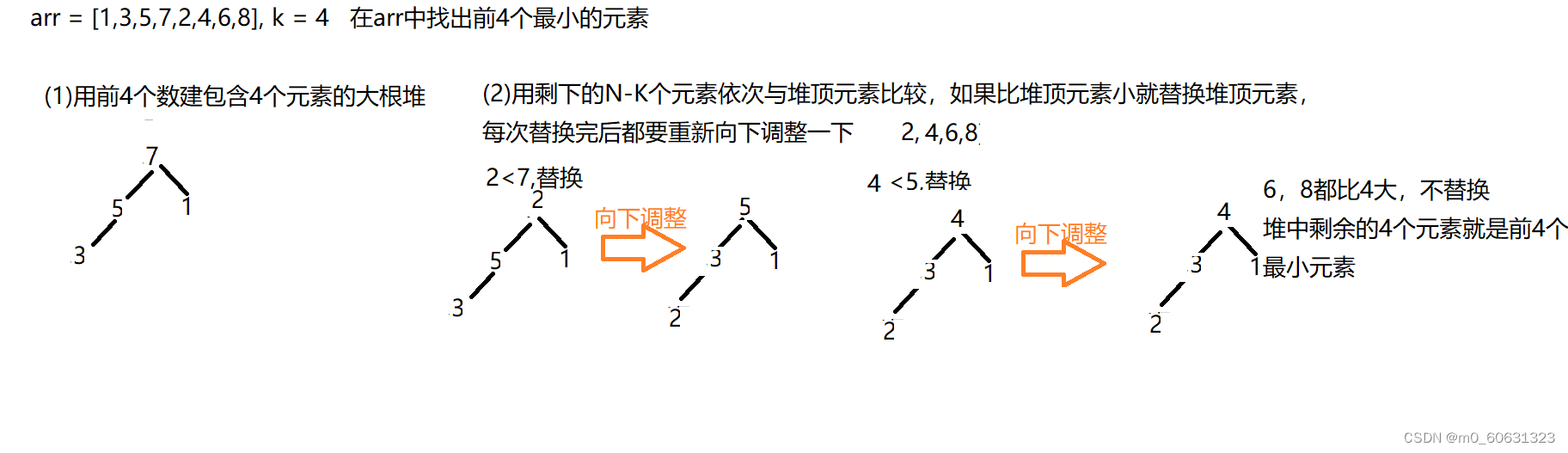
时间复杂度分析:
堆的元素个数为k,故每次向下调整的时间复杂度就是O(logk),总共需要调整n-k次,故总体时间复杂度为O((n-k)logk)
但初次接触Top-k问题的同学肯定这样想过,如果要求的是找出前K个最大的元素,就直接将所有元素建成一个大根堆,然后依次出K个元素就可以了啊!!!
这中做法的确可以,但由于时间复杂度过高而一般不采取
如果对于一个 数组中一共有n个数据,想找前n-1个最大值,那么每次出元素后都要重新调整一下堆,每次向下调整的时间复杂度是O(logn),所以总体的时间复杂度就是O(nlogn);
最小K个数
代码:
public int[] smallestK(int[] arr, int k) {
int[] ret=new int[k];
if(k<=0||k> arr.length){
return ret;
}
PriorityQueue<Integer> maxHeap=new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});
for (int i = 0; i <arr.length; i++) {
if(maxHeap.size()<k){
maxHeap.offer(arr[i]);
}else {
int top=maxHeap.peek();
if(arr[i]<top){
maxHeap.poll();
maxHeap.offer(arr[i]);
}
}
}
for (int i = 0; i < k; i++) {
ret[i]=maxHeap.poll();
}
return ret;
}
前K个高频单词
因为这里用到了map和set,在后续map和set中有详细说明
public static List<String> topKFrequent(String[] words, int k) {
Map<String ,Integer> map= new HashMap<>();
for (String word:words) {
if(!map.containsKey(word)){
map.put(word,1);
}else {
int val=map.get(word);
map.put(word,val+1);
}
}
PriorityQueue<Map.Entry<String,Integer>> minHeap=new PriorityQueue<>(new Comparator<Map.Entry<String, Integer>>() {
@Override
public int compare(Map.Entry<String, Integer> o1, Map.Entry<String, Integer> o2) {
if(o1.getValue().compareTo(o2.getValue())==0){
return o2.getKey().compareTo(o1.getKey());
}
return o1.getValue().compareTo(o2.getValue());
}
});
for (Map.Entry<String ,Integer> entry:map.entrySet()) {
if(minHeap.size()<k){
minHeap.add(entry);
}else {
Map.Entry<String ,Integer> top=minHeap.peek();
Integer val=top.getValue();
if(val.compareTo(entry.getValue())<0){
minHeap.poll();
minHeap.add(entry);
} else if(val.compareTo(entry.getValue())==0){
String key=top.getKey();
if(key.compareTo(entry.getKey())>0){
minHeap.poll();
minHeap.add(entry);
}
}
}
}
List<String> list=new ArrayList<>();
for(int i=0;i<k;i++){
String key=minHeap.poll().getKey();
list.add(key);
}
Collections.reverse(list);
return list;
}
四、堆的应用
4.1堆排序
利用堆的思想进行排序,总共分为两个步骤;
- 建堆
- 升序:建大堆
- 降序:建小堆
- 利用堆删除的思想来进行排序
(1)交换堆顶与堆尾元素,此时usedSize–
(2)向下调整为大根堆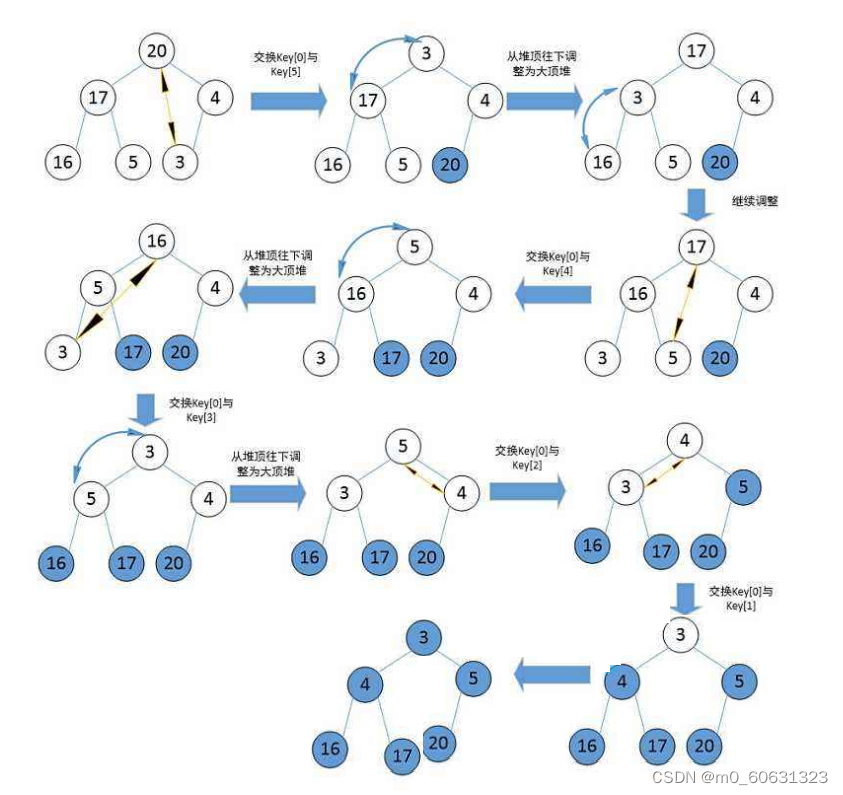
public void heapSort(){
createHeap(array);
int end=usedSize-1;
while(end>0){
int tmp=elem[0];
elem[0]=elem[end];
elem[end]=tmp;
end--;
shiftDown(end);
}
}
时间复杂度:O(n*logn)
边栏推荐
猜你喜欢

微信打开时支持消息通知横幅引热议;Google和甲骨文的云服务因英国高温天气而下线;谷歌发布开源开发语言Carbon|极客头条
Use of doccano data annotation platform
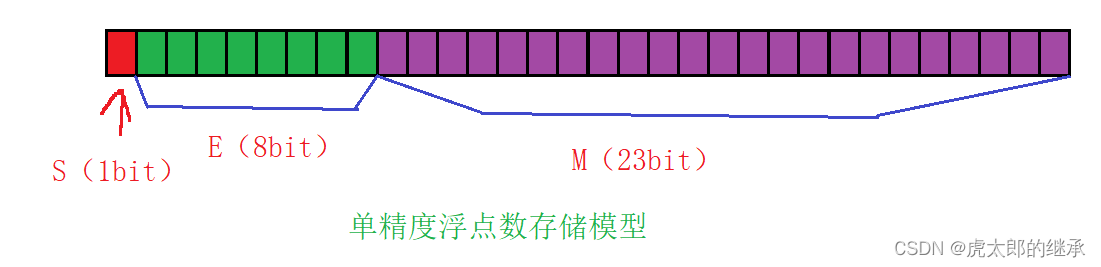
Advanced C language: data storage (floating point)

rexroth比例阀4WRPEH6C3B04L-3X/M/24F1-885

2. ZABBIX concept

2.zabbix概念

Multithreading and high concurrency -- synchronized locking and unlocking process
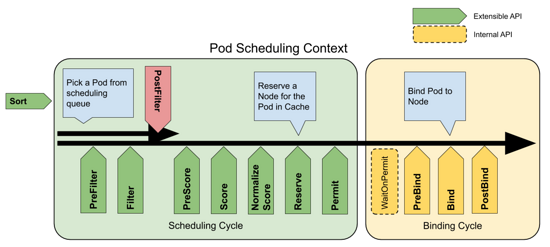
Kubernetes scheduling concept and workflow
![[development of large e-commerce projects] thread pool - completable future -48](/img/15/6e23dac5ac003ecc824f4de90bb0e0.png)
[development of large e-commerce projects] thread pool - completable future -48

08. Use of octave language - control statements, drawing lines and other commands
随机推荐
Typescript数组扩展使用
微信打开时支持消息通知横幅引热议;Google和甲骨文的云服务因英国高温天气而下线;谷歌发布开源开发语言Carbon|极客头条
5.zabbix创建自定义key
Meituan two sides: redis five basic data structures?
The way to practice and play strange: the method of detecting data types in JS
Test cases of common functions
C language: leak detection and filling (II)
8.zabbix分布式
7种 实现web实时消息推送的方案
[ERR] 1273 - Unknown collation: ‘utf8mb4_ 0900_ ai_ ci‘
AttributeError: ‘str‘ object has no attribute ‘param_group‘
The way of practicing and fighting strange things: detailed explanation of sym in ES6
Anomaly detection and self encoder (2)
cookie和seesion的区别和联系
常用功能的测试用例
查找问题:顺序查找与二分法查找
实习打怪之路:JS中检测数据类型的方法
DOM -- event chain (capture target and capture)
解决v-for中el-popover显示等问题
英国天气过热导致谷歌云、Oracle云服务中断

