数学基础系列文章目录

拉格朗日乘子法与KKT条件

一、无约束优化

  对于无约束优化，如果目标函数是凸函数，可直接通过令目标函数的梯度为零求得全局最优值；为避免陷入局部最优值，一般进行优化的目标函数采用凸函数；
  凸集定义：在欧氏空间中，对于集合中任意两点的连线，连线上的点都在集合中，则该集合为凸集合；
  凸函数定义：对于任意属于[0,1]的a和任意属于凸集的x、y，有f[ax+(1-a)x]≤af(x)+(1-a)f(y)，几何意义上就是两点连线上的函数值要大于等于两点之间某点的函数值，即凸函数的任一局部极小点就是全局极小点；
  凸函数的充要条件：有f(x)在开凸集S上具有二阶连续偏导数，且f(x)的海塞矩阵（二阶偏导的矩阵）在S上处于半正定，则f(x)为S上的凸函数；
 

二、带约束优化定义

  带约束的优化问题，形式为
$\{\begin{array}{ll}& minf(x)\\ & s.t.g_i(x)⩽0\\ & h_j=0\end{array}$
  若三个函数都为线性函数，则该问题为线性规划问题；若任意一个函数为非线性函数，则该问题为非线性规划问题；若目标函数为二次函数，且约束函数都为线性函数，则为二次规划；若目标函数和不等式约束函数为凸函数，等式约束函数为线性函数，则该问题为凸优化问题；
 

三、等式约束

 
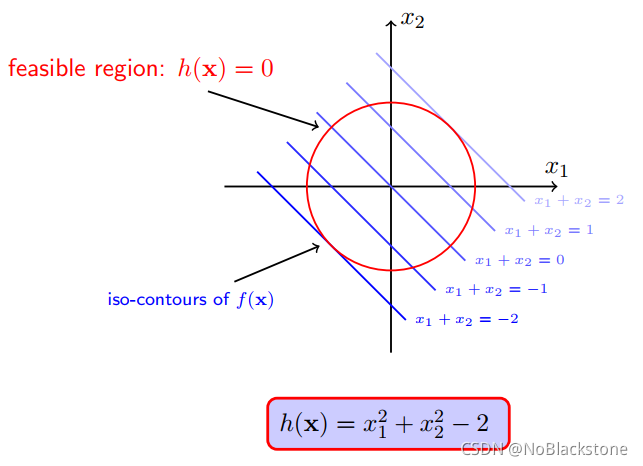
  要在等式约束求得目标函数的极小点，就得找目标函数与约束函数的切点，在切点上可以认为，目标函数的梯度与约束函数的梯度是处于一条直线上的，即存在拉格朗日乘子$\mu ⩾0$，有${\nabla }_{x}f(x^{\ast })=\mu {\nabla }_{x}h(x^{\ast })$；满足前述式子并同时满足等式约束函数为零，就能将带约束的优化问题转为不带约束的优化问题，这就是拉格朗日乘子法；
  对$L(x,\mu )=f(x)+\mu h(x$)求极小值$x^{\ast }$,该极小值需满足以下条件${\nabla }_{x}L(x^{\ast },{\mu }^{\ast })=0$与${\nabla }_{\mu }L(x^{\ast },{\mu }^{\ast })=0$。
 

不等式约束

  对于不等式约束函数，在几何上它表示为一个区域，称为可行域；一般分为两种情况讨论，第一种是极值点落入可行域内（不包含边界）；第二种是极值点落入可行域外（包含边界）；
第一种情况：
  若目标函数的极值点落入可行域内，则约束函数是不起约束作用的，此时可以直接通过令目标函数的梯度为零求得极值点；如图所示：

 
第二种情况：
  当目标函数的极值点落入可行域外时，约束函数就会起到约束作用，而目标函数就需要在约束函数的边界上求得极值点（因为极小值点在边界上，此时约束函数为零），即切点，同理两个函数的梯度会在一条直线上，只是约束函数的梯度会与目标函数的负梯度同向，有$-{\nabla }_{x}f(x)=\lambda {\nabla }_{x}g(x)$ 和$\lambda >0$；如图所示：

 
  总结：根据以上两种情况，构造拉格朗日函数求解问题；对于不等式约束优化问题，满足三个条件的解便是极小值点，它们就是KKT条件，即存在优化问题：$mi{n}_{x}f(x)s.t.g(x)⩽0$；可构造成：$L(x,\lambda )=f(x)+\lambda g(x)$，通过令${\nabla }_{x}L(x,\lambda )=0$和 ${\nabla }_{\lambda }L(x,\lambda )=0$，求得极小值点$x^{\ast }$；其中极小值点需满足KKT条件：${\nabla }_{x}L(x^{\ast },{\lambda }^{\ast })=0$和${\lambda }^{\ast }\ge 0$和${\lambda }^{\ast }g(x^{\ast })=0$；
 

五、约束优化总结

  当同时有多个等式约束和多个不等式约束时，构造拉格朗日函数在目标函数后面将约束函数相应加上，并将所有条件整合到一起；
存在优化问题，$mi{n}_{x}f(x)s.t.h_i(x)=0,g_j(x)⩽0$；
将其构造为，$L(x,\mu ,\lambda )=f(x)+{\mu }^{T}h(x)+{\lambda }^{T}g(x)$；
其中最优解满足条件，${\nabla }_{x}L(x^{\ast },{\mu }^{\ast },{\lambda }^{\ast })=0，{\lambda }_j^{\ast }\ge 0，{\lambda }_j^{\ast }{g}_j(x^{\ast })=0，g_j(x^{\ast })\le 0，h(x^{\ast })=0$；
 

拉格朗日对偶性

  在约束优化问题中，常常使用拉格朗日对偶性将原始问题转为对偶问题，通过求解对偶问题的解得到原始问题的解；
 

一、对偶的可用性

  首先明确，对偶问题的解不一定直接等于原问题的解（弱对偶），但是对偶问题有两点性质：1、满足强对偶条件时，对偶问题的解等于原始问题的解；2、对偶问题一定是凸优化问题；
 

二、原始问题

  原始问题的优化问题有 $\{\begin{array}{ll}& minf(x)\\ & s.t.g_i(x)⩽0\\ & h_j(x)=0\end{array}$；定义拉格朗日函数，$L(x,\alpha ,\beta )=f(x)+{\sum }_{i=1}^q{\alpha }_i{g}_i(x)+{\sum }_{j=q+1}^m{\beta }_j{h}_j(x)$；考虑函数，$\Theta P(x)=\underset{\alpha ,\beta :{\alpha }_i⩾0}{\max }L(x,\alpha ,\beta )$，显然当满足约束时，函数为f(x)，当不满足约束时，函数为正无穷，即 $\Theta P(x)=\{\begin{array}{ll}f(x),& satisfyconstraints\\ +\infty ,& others\end{array}$；极小化该函数得到， $\underset{x}{\min }\Theta P(x)=\underset{x}{\min }\underset{\alpha ,\beta :{\alpha }_i⩾0}{\max }L(x,\alpha ,\beta )$，和原始的优化问题是等价的；同时定义原始问题的最优值为$p^{\ast }=\underset{x}{\min }\Theta P(x)$；
 

三、对偶问题

  考虑函数，$\Theta D(\alpha ,\beta )=\underset{x}{\min }L(x,\alpha ,\beta )$；极大化该函数得到$\underset{\alpha ,\beta :{\alpha }_i⩾0}{\max }\Theta D(\alpha ,\beta )=\underset{\alpha ,\beta :{\alpha }_i⩾0}{\max }\underset{x}{\min }L(x,\alpha ,\beta )$；将该极大化问题视为对偶问题，同时定义对偶问题的最优值为$d^{\ast }=\underset{\alpha ,\beta :{\alpha }_i⩾0}{\max }\Theta D(\alpha ,\beta )$。
 

四、原始问题和对偶问题的关系

  易得$d^{\ast }⩽p^{\ast }$，因为p是先求最大的一块区域然后子啊这块区域求最小，d是先求最小的一块区域然后再这块区域求最大，最大里面的最小，总会大于等于，最小里面的最大；
  对$d^{\ast }⩽p^{\ast }$，称为弱对偶，对于所有优化问题都成立，可得原始问题的下界；如果$d^{\ast }⩽p^{\ast }$，称为强对偶，要满足某些条件才成立；
  如果原始问题是一个凸优化问题，且不等式约束函数是严格可行的，即存在x对所有不等式约束函数都小于零，那么强对偶成立；注意的是，这只是强对偶成立的一种情况，在非凸问题中也可以得到强对偶；
  强对偶成立时，将拉格朗日函数分别对原变量x和对偶变量α,β分别求导，令导数等于零（需要满足KKT条件），即可求解对偶问题的解，同时也求得原始问题的解；
  在对偶问题求解中，如果原始问题不一定是凸优化问题时，在强对偶的情况下，要满足KKT条件；若原始问题是凸优化问题时，则强对偶和KKT条件时互为充要条件的。