当前位置:网站首页>2022/7/ 20 训练记录
2022/7/ 20 训练记录
2022-07-21 15:36:00 【钟钟终】
算法训练
Kruskal算法
P2323 [HNOI2006]公路修建问题
思路:复习了一遍kruskal算法。本题较为复杂,但拆解下来算法中都是常规操作。
1.对一级公路进行排序,跑一遍kurskal算法,当一级公路数量达到k时,则返回退出,记录最大的公路数值;
2.同样,对二级公路排序,再重新写一个kruskal算法,当数量达到n-1-k则退出循环,记录二级公路最大数值;
3.这种做法认真想来是存在问题的,如果k条一级公路选定后数值小于二级公路最大数值,那么可以再继续选1级公路,二级公路则选前面一条公路数值,进行比较,判断出最小;
#include <bits/stdc++.h>
//#define int long long
#define endl '\n'
using namespace std;
const int N=1e5+100;
int n,k,m,f[N],g,minn;
bool vis[N];
struct node
{
int a,b,c1,c2,id;
}e[N];
struct Ans
{
int p,q;
}ans[N];
bool cmp1(node n1,node n2)
{
return n1.c1<n2.c1;
}
bool cmp2(node n1,node n2)
{
return n1.c2<n2.c2;
}
bool cmp3(Ans a1,Ans a2)
{
return a1.p<a2.p;
}
int r_find(int r)
{
if(r==f[r]) return f[r];
f[r]=r_find(f[r]);
return f[r];
}
void kruskal1()
{
int tmp=0;
for(int i=1;i<=m;i++)
{
if(!vis[e[i].id])
{
int fx=r_find(e[i].a),fy=r_find(e[i].b);
if(fx==fy)
continue;
f[fx]=fy;
tmp++,g++;
minn=max(minn,e[i].c1);
ans[g].p=e[i].id;
ans[g].q=1;
}
if(tmp==k)
return;
}
}
void kruskal2()
{
int tmp=0;
for(int i=1;i<=m;i++)
{
if(!vis[e[i].id])
{
int fx=r_find(e[i].a),fy=r_find(e[i].b);
if(fx==fy)
continue;
f[fx]=fy;
tmp++,g++;
minn=max(minn,e[i].c2);
ans[g].p=e[i].id;
ans[g].q=2;
}
if(tmp==n-1-k)
return;
}
}
signed main()
{
cin>>n>>k>>m;
m-=1;
for(int i=1;i<=n;i++)
f[i]=i;
for(int i=1;i<=m;i++)
{
cin>>e[i].a>>e[i].b>>e[i].c1>>e[i].c2;
e[i].id=i;
}
sort(e+1,e+m+1,cmp1);
kruskal1();
sort(e+1,e+m+1,cmp2);
kruskal2();
cout<<minn<<endl;
sort(ans+1,ans+g+1,cmp3);
for(int i=1;i<=g;i++)
{
cout<<ans[i].p<<" "<<ans[i].q<<endl;
}
return 0;
}
Kruskal重构树
代码:分为两个部分,kruskal模板+lca模板
性质: 讲解的的文章
原本图中的n个节点,均为树上的叶子节点;
重构树是一个大根堆(按最小生成树重构);
重构树(按最小生成树重构)中,任意两个节点a,b的,在原图上的路径中的最大边权的最小值为LCA(a,b)的点权;
若原图不连通,会得到重构树森林;
重构树的节点总数为2n−1,它是一个二叉树。
使用场景:可以用来解决一类诸如“查询从某个点出发经过边权不超过val的边所能到达的节点”的问题。
P1967 [NOIP2013 提高组] 货车运输
问题:每条道路对车辆有重量限制,在不超过限重的情况下,最多能运多种的货物?
1.本问题是基于最大生成树,即道路重量限制的排序规则为降序;
2.最近公共祖先Lca的模板,两次dfs。
3.dfs1求出size(子树大小),dep(所在节点深度),fa(父节点),son(x的中儿子);dfs2求出top(x所在重链的顶端)
4.接着重构生成树。共2n-1个点,n-1个点为虚点,n个点是实点。
#include <bits/stdc++.h>
//#define int long long
#define endl '\n'
using namespace std;
const int N=1e5+100;
int n,m,f[N],tol,val[N];
vector<int>g[N];
bool vis[N];
struct node
{
int x,y,z;
}e[N];
bool cmp(node e1,node e2)
{
return e1.z>e2.z;
}
int r_find(int r)
{
if(r==f[r]) return f[r];
f[r]=r_find(f[r]);
return f[r];
}
int son[N],siz[N],top[N],fa[N],dep[N];
void dfs1(int u,int pare) //重构树lca初始化
{
siz[u]=1;dep[u]=dep[pare]+1;
son[u]=0;fa[u]=pare;
for(auto &v:g[u])
{
if(v!=pare)
{
dfs1(v,u);
siz[u]+=siz[v];
if(siz[son[u]]<siz[v])
son[u]=v;
}
}
}
void dfs2(int u,int topf)
{
top[u]=topf;
if(son[u])
dfs2(son[u],topf);
for(auto &v:g[u])
{
if(v!=fa[u]&&v!=son[u])
dfs2(v,v);
}
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
void kruskal()
{
for(int i=1;i<n*2;i++)
f[i]=i;
sort(e+1,e+m+1,cmp);
tol=n;
for(int i=1;i<=m;i++)
{
int fx=r_find(e[i].x),fy=r_find(e[i].y);
if(fx!=fy)
{
val[++tol]=e[i].z;
f[fx]=f[fy]=tol;
g[fx].push_back(tol),g[tol].push_back(fx);
g[fy].push_back(tol),g[tol].push_back(fy);
if(tol ==n*2-1) break;
}
}
for(int i=1;i<=tol;i++)
{
if(!siz[i])
{
int rt=r_find(i);
dfs1(rt,0);
dfs2(rt,rt);
}
}
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
cin>>e[i].x>>e[i].y>>e[i].z;
kruskal();
int q;cin>>q;
while(q--)
{
int u,v;cin>>u>>v;
if(r_find(u)!=r_find(v))
cout<<-1<<endl;
else
cout<<val[lca(u,v)]<<endl;
}
return 0;
}
P2245 星际导航
问题:边权是航行的危险程度,点 A 航行到顶点 B 所经过最危险的边的危险程度值最小可能是多少?
思路:本问题是基于最小生成树,即危险系数的排序规则为生序;
#include <bits/stdc++.h>
//#define int long long
#define endl '\n'
using namespace std;
const int N=5e5+100;
int n,m,q,f[N],tol,val[N];
vector<int>g[N];
struct node
{
int a,b,c;
}e[N];
bool cmp(node e1,node e2)
{
return e1.c<e2.c;
}
int r_find(int r)
{
if(r==f[r]) return f[r];
f[r]=r_find(f[r]);
return f[r];
}
int son[N],siz[N],top[N],fa[N],dep[N];
void dfs1(int u,int pare) //重构树lca初始化
{
siz[u]=1;dep[u]=dep[pare]+1;
son[u]=0;fa[u]=pare;
for(auto &v:g[u])
{
if(v!=pare)
{
dfs1(v,u);
siz[u]+=siz[v];
if(siz[son[u]]<siz[v])
son[u]=v;
}
}
}
void dfs2(int u,int topf)
{
top[u]=topf;
if(son[u])
dfs2(son[u],topf);
for(auto &v:g[u])
{
if(v!=fa[u]&&v!=son[u])
dfs2(v,v);
}
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
void kruskal()
{
for(int i=1;i<n*2;i++)
f[i]=i;
sort(e+1,e+m+1,cmp);
tol=n;
for(int i=1;i<=m;i++)
{
int fx=r_find(e[i].a),fy=r_find(e[i].b);
if(fx!=fy)
{
val[++tol]=e[i].c;
f[fx]=f[fy]=tol;
g[fx].push_back(tol),g[tol].push_back(fx);
g[fy].push_back(tol),g[tol].push_back(fy);
if(tol ==n*2-1) break;
}
}
for(int i=1;i<=tol;i++)
{
if(!siz[i])
{
int rt=r_find(i);
dfs1(rt,0);
dfs2(rt,rt);
}
}
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
cin>>e[i].a>>e[i].b>>e[i].c;
kruskal();
cin>>q;
while(q--)
{
int u,v;cin>>u>>v;
if(r_find(u)!=r_find(v))
cout<<"impossible"<<endl;
else
cout<<val[lca(u,v)]<<endl;
}
return 0;
}
思维训练
A. Doremy’s IQ(div1)
思路:
1.很容易想到,前面参与竞赛的选择会影响后面参与竞赛的数量,即会产生那个后效性。因此应该从后往前进行选择。
2.如果智商为2,从后向前看时:如果有竞赛值大于2,若参与则2降为1,但是对前面的竞赛不构成影响。
3.从后向前,有q次选择是和竞赛要求的值无关,当q消耗完时,前面若有小于等于q的竞赛,则无条件参加。
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1e6+100;
int n,q,a[N];
char c[N];
signed main()
{
int t;cin>>t;
while(t--)
{
cin>>n>>q;
for(int i=1;i<=n;i++)
cin>>a[i],c[i]='0';
int g=0;
for(int i=n;i>=1;i--)
{
if(a[i]<=g) c[i]='1';
else if(g<q)
c[i]='1',g++;
}
for(int i=1;i<=n;i++)
cout<<c[i];
cout<<endl;
}
return 0;
}
D. Difference Array
思路:这题开始做的时候也没啥思路,n个数进行差分,进行n-1次缩减,最后输出a[n]的值,感觉和暴力一样。
1.n-1次缩减是固定的,每轮将a[i]更新为0,不参与排序。
2.若数字相减出的结果为0,则该数字也不应参与排序。因为a[i]和0相减的结果还是a[i],对于排序来说会增加复杂度,算是暴力做法的一个优化。
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1e6+100;
int n,a[N];
signed main()
{
int t;cin>>t;
while(t--)
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
int l=1;
for(int i=1;i<=n-1;i++)
{
for(int j=n;j>=l;j--)
a[j]-=a[j-1];
a[i]=0;
sort(a+l,a+n+1);
while(a[l]==0&&l<=n)
l++;
}
cout<<a[n]<<endl;
}
return 0;
}
边栏推荐
- 索引
- mysql8中timestamp时间戳设置默认值 CURRENT_TIMESTAMP ,Error:1048 - Column ‘createTime‘ cannot be null
- 线性表的实现
- side effect of intrinsics
- The properties of variables and functions beginning with static specifiers in C language
- IO model, multiplexing
- [log4j.properties complete configuration, suitable for beginners]
- 空悬指针和孤儿内存
- 8.026 billion yuan! The state Internet Information Office imposed administrative penalties related to network security review on didi in accordance with the law
- Keras deep learning practice (11) -- visual neural network middle layer output
猜你喜欢

Idea SSH tool remote link failed

How to add a map to a page

Keras深度学习实战(15)——从零开始实现YOLO目标检测

CodeSys中编程实现串口通讯【基于树莓派4B】

Piecemeal knowledge - SQL related

Keras deep learning practice (13) -- detailed explanation of the basis of target detection

VLOOKUP函数
![Steps for installing and using redis [Linux and windows environment]](/img/9e/39a28fa6505374934eb01031928cba.png)
Steps for installing and using redis [Linux and windows environment]
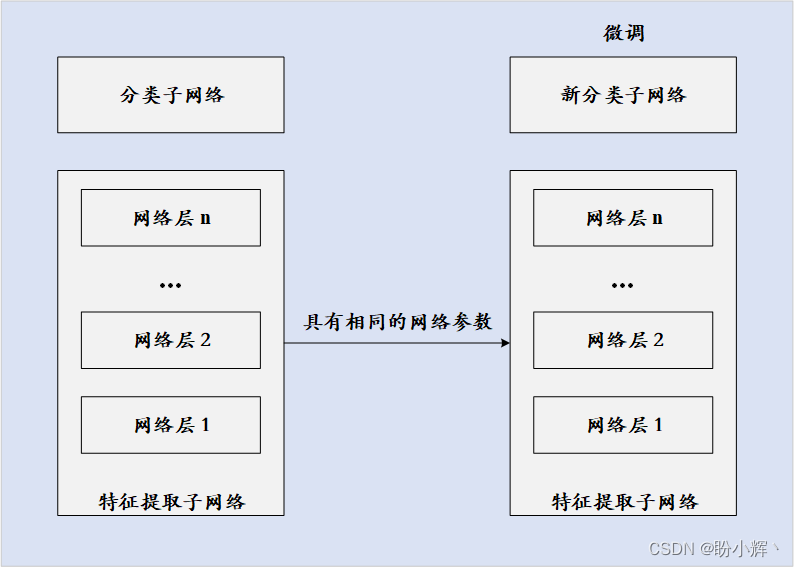
Keras deep learning practice (10) -- transfer learning
20、shell编程之变量
随机推荐
B树与B+树 hash索引
手机对比redmi note8与realme x2
Matlab GUI programming skills (VIII): uitoolbar create toolbar in the drawing window
Implementation of linear table
Piecemeal knowledge - statistical correlation
Matlab GUI programming skills (IX): explain the uitable function display table and related operations in detail (create table user interface)
Keras深度学习实战(11)——可视化神经网络中间层输出
Indexes
Oracle 关于date 字段索引使用测试
可视化之基础设置
关于mysql驱动版本报错解决,Cause: com.mysql.jdbc.exceptions.jdbc4、Unknown system variable ‘query_cache_size
软件推荐-装机
[caused by: com.mysql.jdbc.exceptions.jdbc4.mysqlsyntaxerrorexception: SQL statement parameters are different from methods]
[log4j.properties configuration full version]
Scala函数及其高阶应用
Debian 全版本更换镜像源为阿里云镜像源
VLOOKUP函数
Keras深度学习实战(13)——目标检测基础详解
吃了爱优腾的药,奈飞病情好转
[log4j.properties complete configuration, suitable for beginners]