当前位置:网站首页>正则表达式相关
正则表达式相关
2022-07-22 04:28:00 【傲然*】
文章目录
正则表达式
简介
- 正则表达式是对字符串(包括普通字符(例如,a 到 z 之间的字母)和特殊字符(称为“元字符”))操作的一种逻辑公式,就是用事先定义好的一些特定字符及这些特定字符的组合,组成一个“规则字符串”,这个“规则字符串”用来表达对字符串的一种过滤逻辑。正则表达式是一种文本模式,该模式描述在搜索文本时要匹配的一个或多个字符串。
- 构造正则表达式的方法和创建数学表达式的方法一样。也就是用多种元字符与运算符可以将小的表达式结合在一起来创建更大的表达式。正则表达式的组件可以是单个的字符、字符集合、字符范围、字符间的选择或者所有这些组件的任意组合
语法综述
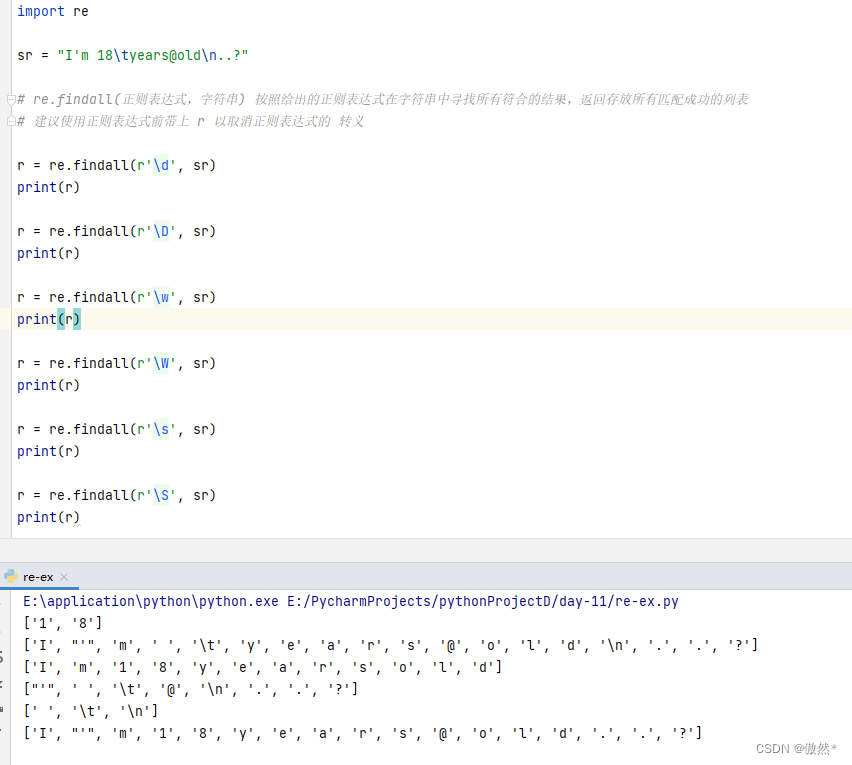
| 元字符 | 描述 |
|---|---|
| . | 匹配单个任意除换行符之外的符号 |
| \d | 匹配单个数字 |
| \D | 匹配单个非数字,包括字母、标点符号、空格、换行等 |
| \w | 匹配单词字符,包括大小写字母和数字 |
| \W | 匹配非单词字符。包括标点符号、空格换行等 |
| \s | 匹配空格、换行符、换页符、制表符等空白字符 |
| \S | 匹配非空白字符 |
| […] | 字符集,对应位置可是字符集内的任意某个字符;字符集中的字符可以单个列出如:[abcd],也可以给出范围如:[a-d];如果第一个字符是 ^ 表示取反,如:[^a] ,表示不是a的其他字符 |
| 量词(用在元字符或(…)之后的) | |
| ? | 匹配前一个字符0次或1次 |
| * | 匹配前一个字符0次或无限次 |
| + | 匹配前一个字符1次或无限次 |
| {m} | m 是一个非负整数,匹配前一个字符m次 |
| {m,} | m 是一个非负整数,匹配前一个字符至少m次 |
| {m,n} | m 、n是一个非负整数,匹配前一个字符最少m次,最多n次 |
| *?、+?、{m.n}? | 使 *、+、{m,n}变为非贪婪模式 |
| \b | 匹配单词边界,字符串的开始与结尾处称为单词边界,字符串可以包括字母和数字 |
| \B | 匹配非单词边界 |
| ^ | 匹配输入字符串开头的位置 |
| $ | 匹配输入字符串结尾的位置 |
| 分组 | |
| (…) | 将括起来的表达式称为分组,从表达式左边开始每遇一个分组的(,分组编号+1,分作作为一个整体,后面可接数量词 |
| \num | 可以引用分组,num为分组的编号 |
| 断言 | |
| x(?=y) | 先行肯定断言,仅当x后面为y时匹配x |
| (?<=y)x | 后行肯定断言,仅当x前面为y时匹配x |
| x(?!y) | 先行否定断言,仅当x后面不为y时匹配x |
| (?<!y)x | 后行否定断言,仅当x前面不为y时匹配x |
模式修正符
| 修饰符 | 说明 |
|---|---|
| i | 忽略大小写 |
| m | 多文本模式 |
| s | 单行文本模式 |
| x | 忽略空白字符 |
| U | 表示拒绝贪婪匹配 |
| g | 表示全局匹配 |
元字符
- 正则表达式是由普通字符(例如字符 a 到 z)以及特殊字符(称为"元字符")组成的文字模式。普通字符包括没有显式指定为元字符的所有可打印和不可打印字符。这包括所有大写和小写字母、所有数字、所有标点符号和一些其他符号。
- 所谓特殊字符,就是一些有特殊含义的字符,要求在试图匹配它们时特别对待。若要匹配这些特殊字符,必须首先使字符"转义"
量词
- 量词用来指定正则表达式的一个给定组件必须要出现多少次才能满足匹配

元组
()将一个或多个字符捆绑在一起,当作一个整体进行处理,分组括号中的模式匹配到的内容会被正则表达式引擎记录于内部的变量中,这些变量的命名方式为:\1, \2, \3。对于分组而言,整个表达式永远算作\0- 后向引用:引用前面的分组括号中的模式所匹配字符,而非模式本身,\1 表示从左侧起第一个左括号以及与之匹配右括号之间的模式所匹配到的字符,\2 表示从左侧起第2个左括号以及与之匹配右括号之间的模式所匹配到的字符,以此类推,& 表示前面的分组中所有字符。

- 非捕获组
(?:Pattern);它的作用就是匹配Pattern字符,但不捕获文本,不将匹配到的字符存储到内存中,从而节省内存
重复分组
- 用
(\d\d\d){3}去匹配1234567890,开始我以为分组小括号(\d\d\d)的最终结果是123,456,789都能拿到,但结果却只有789
- 重复分组的匹配在每次引擎退出该分组的时候被捕获,并会覆盖该分组在之前匹配的任何文本
模拟一下引擎工作的步骤:
- 第一次匹配,捕获到
123,退出分组- 第二次匹配,捕获到
456, 覆盖上一次捕获的123,退出分组- 第三次匹配,捕获到
789,覆盖上一次捕获的456,退出分组- 退出重复分组,结束
- 如果想要获得所有结果,就要把重复匹配放进分组中
/((\d\d\d){3})/
断言
- 先行肯定断言:
x(?=y),仅当x后面为y时匹配x,y不作为返回结果。
- 后行肯定断言:
(?<=y)x,仅当x前面为y时匹配x,y不作为返回结果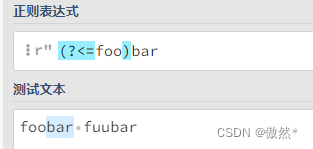
- 先行否定断言:
x(?!y),仅当x后不为y时匹配x,y不作为返回结果
- 后行否定断言:
(?<!y)x,仅当x前面不为为y时匹配x,y不作为返回结果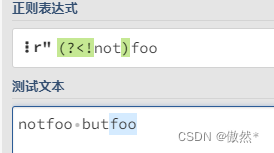
位置锚定
行定位符
^和$可以用来指定开头和结尾,^\d.*就是任意以数字开头的字符串,.*\d$是任意以数字结尾的字符串,^&表示空行- 在使用正则限制长度输入时,如果只使用
{m,n},在输入的长度小于m时,匹配失败,但如果输入的长度大于n,由于其中包含m为,所以会匹配成功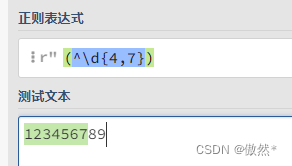
- 为了限制长度可以结合
^和$使用,^\d{4,7}$可以限制输入4到7位数字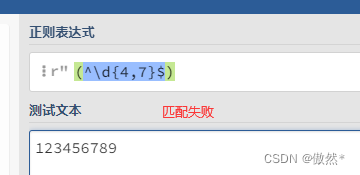
单词边界
\b用来匹配单词的边界,这里的单词指定是\w+,至于边界是什么,如下图,
\b属于匹配位置的元字符,一般作占位作用,而不被捕获,同属于匹配位置的还有匹配行起始位^和行结束位`$
贪婪、非贪婪与回溯
- 当使用
*、+、{m,n}量词时,就涉及到贪婪与非贪婪的匹配模式,例如*是匹配任意除换行符外的字符,如果贪婪模式下,它会一次性匹配所有可以匹配上的字符;而如果是非贪婪模式下,它会尽可能少的匹配。 - 如对于
pythonnnnnnnnnnn这样一个字符串,贪婪模式下使用python*进行匹配,使用量词时默认位贪婪模式,结果如下,可以看出所有n都被匹配
- 而在非贪婪模式下匹配,在量词后面添加
?改为非贪婪模式,匹配结果如下,由于*匹配0次或多次,最少是0次,非贪婪模式下一个n都没有被匹配。
回溯
- 当使用量词导致当前前面分支/重复匹配成功后,没有多余的文本可被正则后半部分匹配时,会产生回溯;如使用
.*\d进行匹配,.*将所有字符匹配完成后,还有个\d需要匹配,此时就会产生回溯 - 用一个简单的例子来解释一下贪婪匹配和惰性匹配的回溯,贪婪 :
/\d+\b/,惰性 :/d+?\b/,文本 :1234a
贪婪正则匹配
1234a时的过程是这样的:
- \d+ 匹配得到 1234
- \b 却匹配失败(\b 是分词边界匹配,用来获取位置,而不是文本)
- 这个时候,\d+会尝试回吐一个字符,即匹配结果为 123 ,可\b还是匹配失败!
- 那就继续回吐,一直到 1,还是匹配失败,那么这个正则就整体匹配失败了
- 这个回吐匹配结果的过程就是回溯
惰性正则匹配
1234a时的过程是这样的:
- \d+? 首先匹配,结果是1 ,紧接着 \b 匹配失败
- 那就 \d+? 继续匹配,结果是 12 ,紧接着 \b 还是匹配失败
- \d+? 一直匹配到1234,紧接着的 \b 依然匹配失败
- 结果整个正则匹配不成功
正则使用案例
千分位
- 我们在一些场景里需要将7654321输出成7,654,321这样的格式,这就是千分位
- 用正则表达式去处理的话,关键是获取位置,那么首先想到的就是要利用非单词边界\B
- 这条正则是能成功取得千分位的位置的:
"\B(?=(\d{3})+(?!\d))"g
先将这个正则分成三个部分:
/\B(?=\d)/这里·\B是为了防止出现,123起始位置被匹配的问题,(?=\d)是非单词边界后紧跟数字
尝试一下8位数的数字: ‘12345678’ 在/\B(?=(\d{3})+)/匹配得到什么结果呢?
最后 (?!\d) 是前面匹配成功后跟的非数字
- ‘12345678’ 在
/\B(?=(\d{3})+)/匹配得到什么结果呢?
首先符合非单词边界
\B的有1,2,3,4,5,6,7的右边位置
然后在\B后还得有n个3位数
匹配结果为:
匹配\B第1个非单词边界1的右边位置,则后面(\d{3})+的结果为:234、567,8后面无法补齐3位,匹配得到567
匹配\B第2个非单词边界2的右边位置,则后面(\d{3})+的结果为:345、678,匹配得到678
匹配\B第3个非单词边界3的右边位置,则后面(\d{3})+的结果为:456、78后面无法补齐3位,匹配得到456
匹配\B第4个非单词边界4的右边位置,则后面(\d{3})+的结果为:567、8后面无法补齐3位,匹配得到567
匹配\B第5个非单词边界5的右边位置,则后面(\d{3})+的结果为:678
匹配\B第6个非单词边界6的右边位置,但78无法补齐3位,
匹配\B第6个非单词边界7的右边位置,但8无法补齐3位,
最终小括号分组匹配得到的分别是:567,678,456,567,678
- 最后 (?!\d) 是前面匹配成功后跟的非数字,那连起来就是:
- 匹配
\B第1个非单词边界1的右边位置,则后面(\d{3})+的结果为:234、567,后面跟着8,不匹配- 匹配
\B第2个非单词边界2的右边位置,则后面(\d{3})+的结果为:345、678,后面跟着非数字,位置匹配成- 匹配
\B第3个非单词边界3的右边位置,则后面(\d{3})+的结果为:456,后面跟着7、8不匹配- 匹配
\B第4个非单词边界4的右边位置,则后面(\d{3})+的结果为:567,后面跟着8,不匹配- 匹配
\B第5个非单词边界5的右边位置,则后面(\d{3})+的结果为:678,后面跟着非数字,位置匹配成功- 最终得到得到可插入逗号的位置为2,5
12,345,678
限制用户密码
- 通常用户在注册时,我们为了提高安全性,会在用户设置密码时添加一些限制,比如密码中必须包含小写字母、大写字母、数字、特殊符号、长度限制等,通常这种限制都是通过正则表达式实现的,这里我们一起探究下正则是如何实现这种限制的
- 首先我们要求用户密码中必须包含数字,这如何限制?通过
(?=\d)可以限制字符中必须包含数字,该断言没有x部分即代表x是所有字符,包括边界;当某个字符或边界后面有数字时,匹配成功。 - 也可以用
\b(?=.*\d)限制字符中必须包含数字,该表示中\b匹配到字符的首单词边界时,当且仅当任意位字符后有数字匹配成功 - 同理得
(?=.*\d)(?=.*[a-z])(?=.*[A-Z]),可以限制密码必须包含数字、小写字母、大写字母,其他同理 - 那如何限制用户长度呢?断言匹配完成后,可以通过
[0-9a-zA-Z]{8,16}限制密码的长度为8到16位 - 最终表达式为
^(?=.*\d)(?=.*[a-z])[a-z0-9]{8,16}$
正则与安全
防止sql注入与绕过
- 打开sqsllab的第一关,我们首先在第一关的php文件中添加过滤语句
# 对用户输入的id进行正则匹配,若匹配到说明存在sql注入
if(preg_match('/select\b[\s\S]*\bfrom/is',$id)){
die('SQL INJECTION');
}
- 在页面输入sql语句进行测试

- 分析绕过:正则对select\b[\s\S]\bfrom``进行匹配,可以看出表达式中的select的后面和from的前面必须有单词边界,可以从这里下手,使用科学技术法绕过,原理为如下图,将1e1加到from前破坏单词边界使匹配失败

- 测试发现依然报错

- 原因是添加了1e1后产生了两列,而这里期望的结果只有一列

- 修改表达式,绕过成功

- 回溯绕过,由于该正则采用了量词的贪婪匹配,我们可以利用回溯绕过限制,php的回溯次数不能大于一百万次,否则匹配失败,所以我在我需要注入的语句后加入一百万个被注释的a,由于是贪婪匹配,将一百万个a全部匹配,然后回溯匹配边界符,由于回溯次数大于一百万,匹配失败,所以注入成功

利用回溯绕过正则限制
案例1
- 如下语句是为了过滤一句话木马的表达式,最简单的一句话木马为
<?php @eval(&_POST('input'));
<?php
function is_php($data){
return preg_match('/<\?.*[(`;?>)].*/is', $data);
}
if(isset($_POST['input'])){
$input=$_POST['input'];
}
if(!is_php($input)){
echo 'flag';
}
- 为了绕过该正则,我们可以利用回溯,php中限制正则回溯的次数为一百万次,超过这个次数则认为是匹配失败,可以看出代码中是利用了贪婪模式进行匹配,所以我们可以向php发送一段这样的输入:在
<?php eval(&_POST('input'));后添加一百万个a - 通过python向后端发送post请求

- 运行后成功将一句话木马传到后端

案例2
- 依据是使用sqllab的第一关环境,添加下述语句,对接收到的参数进行正则匹配
if(preg_match('/union.+?select/is',$id)){
die('SQL INJECTION');
}
- 可以看出表达式是用来过滤联合查询的,由于它使用了
+进行匹配,所以我依然利用回溯绕过,由于是非贪婪匹配,所以我们需要在union和select之间添加一百万个注释a,非贪婪模式下会对一百万个a一个一个的尝试,python代码如下:
案例3
- 后端语句如下:对
Merry Christmas进行过滤,要求正则匹配失败且Merry Christmas仍存在输入中
<?php
function areyouok($greeting){
retunr preg_match('/Merry.*Christmas/is',$greeting);
}
%greeting=$_POST['greeting'];
if(!areyouok($greeting)){
if(strops($greeting,'Merry Christmas')!==false){
echo 'flag'
}else{
echo 'die';
}
}else{
echo 'do you know php';
}
- 由于是量词的贪婪模式进行匹配,同理在
Merry Christmas后加一百万个a,测试结果如下:
- 本案例还有一个绕过方式,strpos()函数如果接受到一个数组作为参数,会返回null,null 和 false 严格不相等,所以绕过

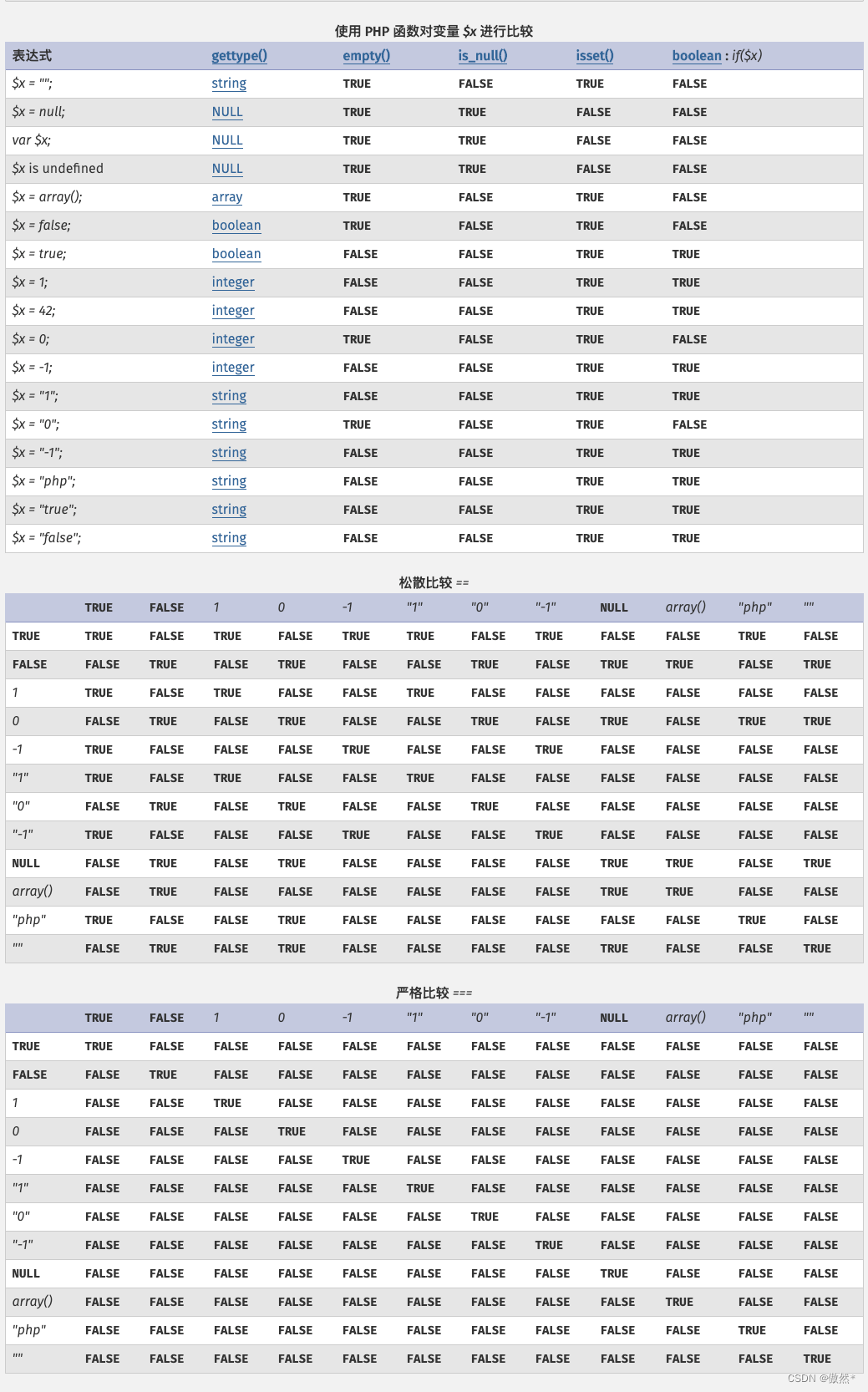
php类型比较
边栏推荐
- 高数_第2章多元函数微分学_隐函数的偏导数
- A Mobile Telematics Pattern Recognition Framework for Driving Behavior Extraction
- C # upload pictures to shared folder
- Screen command use
- Win10系统打开什么都是反应比平时慢,转圈等待1分钟如何解决?
- Informatics Olympiad all in one 1974: [16noip popularization group] palindrome date | Luogu p2010 [noip2016 popularization group] palindrome date
- Popular science | how to create a Dao?
- Figure calculation - figure introduction
- Rquestmapping's annotation function, annotation usage range, and attribute details of annotations
- C # upload files to shared folders
猜你喜欢
![[leetcode weekly race -- hash table number pairs] 6164. Maximum sum of digit and equal number pairs](/img/b1/ad1f0d90e83fa0dfffdb13c3c02e8c.png)
[leetcode weekly race -- hash table number pairs] 6164. Maximum sum of digit and equal number pairs

string的模拟实现

左耳朵耗子:云原生时代的开发者应具备这5大能力

洛谷_P1112 波浪数_思维_进制 / 构造 / 枚举

Mock simulates data and initiates get and post requests (nanny level tutorials are sure to succeed)
![[leetcode stack and queue -- minimum stack] 155. Minimum stack](/img/45/489694b30b0bb75d9799c0acea40cd.png)
[leetcode stack and queue -- minimum stack] 155. Minimum stack
数据平台数据管理实践
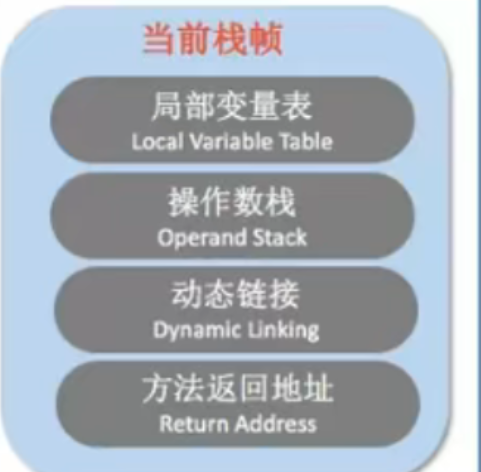
JVM memory model: virtual machine stack
梅科尔工作室——HarmonyOS应用开发培训第三次作业
When the easycvr platform cascades, there is an error prompt. What is the reason why the port is unreachable?
随机推荐
The competition of trillion market value public chain is white hot. Is there still a chance for the new public chain?
Leetcode 172. zero after factorial
Distributed scheduling problem
【Unity】 UI跟随3D物体,世界坐标转UI坐标
梅科尔工作室——HarmonyOs第二次作业
ECCV 2022 | fix the performance damage of large targets caused by FPN: you should look at all objects
嵌入式IDE原理 OpenOCD介绍 以及stlink如何连接stm32板子
AT5662 [AGC040D] Balance Beam(二分)
JVM memory model: runtime data area and thread
博途PLC和ABB变频器PN通讯详解
进程和线程面试问题
Popular science | how to create a Dao?
Leetcode 234. palindrome linked list
Remember a composer dependency problem requires composer runtime API ^2.0.0 - > no matching package found
Detailed explanation of PN communication between botu PLC and ABB Inverter
Mock simulates data and initiates get and post requests (nanny level tutorials are sure to succeed)
交换机与路由器技术:标准ACL、扩展ACL和命名ACL
Pixels and colors
At5662 [agc040d] balance beam (two points)
The principle of embedded IDE, openocd introduction and how stlink connects STM32 board