Heap - principle to application - heap sort, priority queue

Introduction au tas

• Arbre binaire complet：L'arbre binaire complet est l'arbre binaire complet qui est enlevé à la finNArbre après noeuds（$N\ge 0,N\in N^{\ast }$）
• Gros tas de racines：Le noeud parent du noeud est plus grand que le noeud lui - même,Par exemple, la valeur du noeud racine est$8$,Plus que ses enfants $7$, $6$Grand,Le reste est similaire.

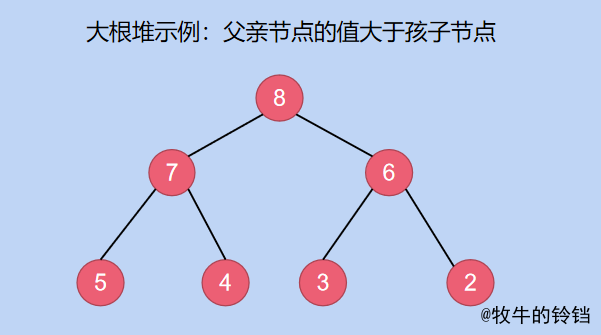
• Petit tas de racines：Le noeud parent du noeud est plus petit que le noeud lui - même,Par exemple, la valeur du noeud racine est$1$,Plus que ses enfants$2$, $3$La valeur de,Le reste est similaire..

Mise en œuvre du tas

Comment stocker un tas

Le stockage en tas est réalisé à l'aide d'un tableau ,Indice de0 De gauche à droite de haut en bas ,Augmentation séquentielle, Par exemple, le petit tas racine ci - dessus stocké dans un tableau est

[1, 2, 3, 4, 5, 6, 7]

L'indice correspondant est $0,1,2,3,4,5,6$

Comment transformer un tableau en tas

Depuis le dernier noeud avec des enfants （ L'indice du noeud est $M$）Début de l'élément, Changez d'abord le Sous - arbre avec l'élément comme noeud racine en tas , Et l'indice diminue $1$, Et l'indice est $M-1$ Le noeud correspondant au sous - arbre devient un tas , En ordre décroissant ,Jusqu'au noeud racine.Voici quelques exemples（Prenons par exemple le petit tas racinaire）：

• Trouver le premier avec un noeud Enfant ,C'est facile à voir à partir de l'image ci - dessus, La valeur du premier noeud enfant est $5$,Son indice est$3$, Son Sous - arbre correspondant est ：

  

  Si vous devez transformer le Sous - arbre supérieur en un petit tas de racines ,Il suffit de$5$Et$1$ Les noeuds correspondants peuvent être échangés （Pas avec$2$Remplacer,Si et$2$Remplacer $2>1$ Ne correspond pas aux propriétés du petit tas racinaire ）, Le résultat est: ：

  

• Puis soustrayez l'indice $1$,C'est - à - dire:$2$,L'élément correspondant est$6$, Maintenant vous devez aussi transformer son Sous - arbre en un petit tas de racines ,C'est - à - dire qu'il faut$6$Et$2$Swap, Le résultat de l'échange est ：

  

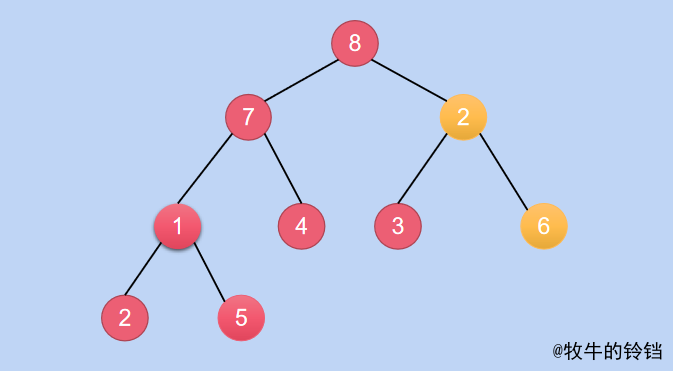
• Continuer à réduire l'indice $1$,Et faire la même chose, Il est facile de savoir $7$Et$1$Changer de position, Le résultat de l'échange est ：

  

Comme vous pouvez le voir sur la photo ci - dessus ,Quand$1$Et$7$Après l'échange,Sous - arbre$[7,2,5]$ Pas un petit tas de racines. ,Et alors?？ Sous - arbre $[7,2,5]$ C'est un tas de racines. , Donc une autre petite opération de tas de racines serait juste ,Oui.$7$, $2$Il suffit d'échanger, Le résultat de l'échange est ：

Dans l'arbre ci - dessus , Le processus d'échange est terminé , Mais si le nombre de noeuds est très grand , Ou que se passe - t - il si le Sous - arbre ci - dessous ne correspond pas à un petit tas de racines? ？ Alors continuez à circuler. , Jusqu'à ce qu'il n'y ait pas de noeud d'enfant ou que la nature du petit tas racinaire soit satisfaite . Nous définissons ce qui précède comme suit: Naufrage(down)Fonctionnement

• Enfin, les noeuds $8$Effectuer les opérations connexes,Les résultats sont les suivants:：

  

• Empiler ensuite les sous - arbres $(heapify)$Fonctionnement:

  

• En cours de gerbage ,Obtenir le résultat final

  

C'est le processus de transformation d'un arbre binaire complet en un petit tas de racines. , Le processus de la Grande pile de racines est très similaire , Le plus grand nombre peut être utilisé comme noeud parent , Pas de déclaration ~~~

Mise en œuvre du Code

Tout d'abord, nous savons que la structure de stockage du tas est un tableau , Il y a donc un indice correspondant , Quelle est la relation entre la position du noeud père et celle du noeud enfant? ？

Si l'indice du noeud parent est $i$ Donc l'indice correspondant pour être un enfant est $2\ast i+1$ L'indice correspondant à l'enfant droit est $2\ast i+2$, Si l'indice du noeud enfant est $i$, L'indice du noeud parent correspondant est $\lfloor \frac{i-1}{2}\rfloor$, Les calculs peuvent être effectués en se référant à l'illustration suivante: .

D'après l'analyse ci - dessus, nous pouvons savoir , Si vous voulez transformer un tableau en tas , Il faut commencer par le dernier noeud avec des enfants. NaufrageFonctionnement,Jusqu'au noeud racine.

NaufrageLes étapes spécifiques de l'opération, Si c'est un petit tas de racines, , Compare la valeur du noeud courant avec les noeuds enfants gauche et droit ,Si le noeud actuel$V$ S'il est plus petit que les noeuds gauche et droit de l'enfant, il s'arrête , Ou le noeud actuel s'arrête sans noeud Enfant , Si la valeur du noeud enfant est inférieure à celle du noeud courant , Vous devez sélectionner la plus petite valeur du noeud Enfant , Puis échangez avec le noeud courant , Et après le déplacement $V$ Refaire ce qui précède . S'il s'agit d'un grand tas de racines, sélectionnez la plus grande valeur dans le noeud Enfant .Les codes spécifiques sont les suivants:：

#include <cstdio>
#include <cstring>
#include <stdlib.h>
#include <time.h>

#define True 1
#define False 0
#define NUM 9
#define MAX_VALUE 100

void swap(int * array, int idx1, int idx2) {
    
    /* Échanger deux éléments d'un tableau */
    int t = array[idx1];
    array[idx1] = array[idx2];
    array[idx2] = t;
}

void down(int * array, int length, int start, int big=False) {
    
    /* array  Est un tableau de tas ,length Est la longueur du tableau,start  Est l'indice de l'élément actuellement à couler ,big  Indique s'il s'agit d'un grand tas racine  */
    while(start < length) {
    
        int left_child = 2 * start + 1;
        int right_child = 2 * start + 2;
        int idx = left_child;
        if (left_child > length - 1)
            /*  Si l'indice correspondant à l'enfant dépasse le nombre d'éléments du tableau, vous devez sauter de la boucle  */
            break;
        if(right_child < length) {
    
            if (!big) {
    
                if(array[right_child] < array[left_child])
                    idx = right_child;
            } else {
    
                if(array[right_child] > array[left_child])
                    idx = right_child;
            }
        }
        if(!big) {
    
            if(array[start] > array[idx]){
    
                swap(array, idx, start);
                start = idx;
            } else{
    
                break;
            }
        } else {
    
            if(array[start] < array[idx]){
    
                swap(array, idx, start);
                start = idx;
            } else{
    
                break;
            }
        }
    }
}

/*  Définir le processus de tas pour l'ensemble du tableau  */
void heapify(int * array, int length, int start=-2, int big=True) {
    
	/* start La valeur par défaut pour est -2  La représentation commence par le dernier élément avec un noeud Enfant  */
    if(start == -1) 
        /* L'indice du dernier élément est0 Encore moins.1Oui.-1  Définir la sortie récursive ici */
        return;
    if (start == -2) {
    
        start = (length - 2) / 2;
    }
    down(array, length, start, big);
    /*  Après le naufrage de l'élément courant   Encore une fois sur son dernier élément  Opération de naufrage*/
    heapify(array, length, start - 1, big);
}

int main() {
    
    int data[NUM] = {
    0, 1, 2, 3, 4, 5, 6, 7, 8};
    heapify(data, NUM);
    for(int i=0; i < NUM; i++) {
    
        printf("%d ", data[i]);
    }
    return 0;
}
/* output : 8 7 6 3 4 5 2 1 0 */

Application du tas

Tri du tas

Pour les tableauxarray = {0, 7, 3, 5, 1, 6, 2, 4, 8} Le tas correspondant est indiqué dans la figure ci - dessous. , Si vous voulez utiliser le tri heap , Il faut d'abord transformer le tableau en tas ,Utilisez ce qui précèdeheapifyFonction.

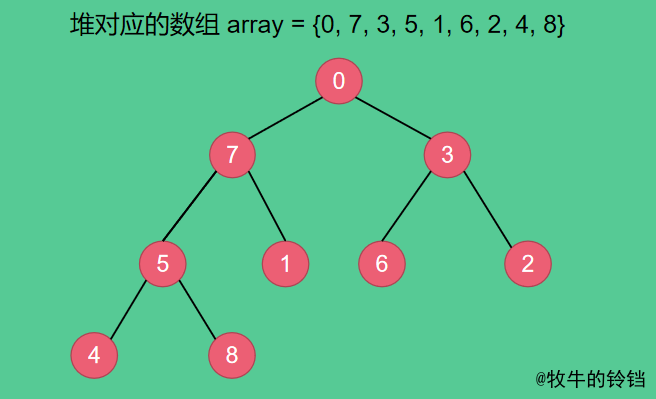
Changez d'abord le tableau en grand tas racine , Le processus de transformation est illustré dans la figure ci - dessous. ：

Les grandes piles de racines qui en résultent Fig.7Comme indiqué. Comment trier après avoir obtenu un grand tas de racines ？ On sait que pour un grand tas de racines , Les noeuds des enfants du noeud racine sont plus petits que lui , Donc le noeud racine doit être l'élément le plus grand du tas , Maintenant, changez la position du noeud racine et du dernier noeud , Les résultats du remplacement sont présentés dans la figure ci - dessous. ：

Vous avez maintenant le plus grand élément du tableau au dernier élément du tableau , Maintenant, on enlève le dernier élément du tas , Pour cette opération, il suffit de réduire la longueur du tas 1, Aucune modification n'est nécessaire pour les données stockées dans le tableau , C'est - à - dire que seuls les éléments du tas {0, 7, 6, 5, 1, 3, 2, 4}, Mais l'élément réel dans le tableau est toujours {0, 7, 6, 5, 1, 3, 2, 4, 8}. Maintenant pour les éléments 0En coursNaufrageFonctionnement. Le processus de fonctionnement est illustré dans la figure ci - dessous. ：

Et ça finira par arriver. V,Parce que les éléments8 Il n'est plus dans la pile. ,Donc pas avec8Remplacement, De sorte que le plus grand élément du tas soit à la dernière position du tableau , Effectuer ensuite l'opération ci - dessus sur le tas constitué des éléments restants , Et placez le plus grand de ces éléments dans l'avant - dernière position , Puis l'élément du noeud racine NaufrageFonctionnement, Ce faisant, il sera possible d'établir l'ordre . Le processus est illustré dans la figure ci - dessous. ：

Enfin, le dernier tas （Il n'y a que deux éléments） Changez de position. , Donc vous obtenez un tableau ordonné . De ce qui précède, nous avons constaté que , Si le tas initial est un grand tas racine, nous obtenons un tableau ascendant , S'il s'agit d'un petit tas de racines, ce sera un tableau descendant .

Mise en œuvre du Code de tri du tas

À partir de ce processus d'analyse, vous pouvez déplacer le noeud racine et le dernier noeud du tas à chaque fois , Puis réduire la longueur du tas 1, Puis les éléments du noeud racine du tas NaufrageC'est bon.,Continue comme ça., Jusqu'à ce qu'il n'y ait qu'un seul élément dans le dernier tas ,Le tri est terminé.Les codes spécifiques sont les suivants:：

#include <cstdio>
#include <cstring>
#include <stdlib.h>

#define True 1
#define False 0
#define NUM 9

void swap(int * array, int idx1, int idx2) {
    
    /*  Échanger deux éléments d'un tableau  */
    int t = array[idx1];
    array[idx1] = array[idx2];
    array[idx2] = t;
}

void down(int * array, int length, int start, int big=False) {
    
    while(start < length) {
    
        int left_child = 2 * start + 1;
        int right_child = 2 * start + 2;
        int idx = left_child;
        if (left_child > length - 1)
            break;
        if(right_child < length) {
    
            if (!big) {
    
                if(array[right_child] < array[left_child])
                    idx = right_child;
            } else {
    
                if(array[right_child] > array[left_child])
                    idx = right_child;
            }
        }
        if(!big) {
    
            if(array[start] > array[idx]){
    
                swap(array, idx, start);
                start = idx;
            } else{
    
                break;
            }
        } else {
    
            if(array[start] < array[idx]){
    
                swap(array, idx, start);
                start = idx;
            } else{
    
                break;
            }
        }
    }
}

void heapify(int * array, int length, int start=-2, int big=True) {
    

    if(start == -1)
        return;
    if (start == -2) {
    
        start = (length - 2) / 2;
    }
    down(array, length, start, big);
    heapify(array, length, start - 1, big);
}


void heap_sort(int * array, int length, bool reverse=False) {
    
    for(int i = length - 1; i >=0; i--) {
    
        swap(array, i, 0);
        down(array, i, 0, !reverse);
    }
}

int main() {
    
    int data[NUM] = {
    0, 7, 3, 5, 1, 6, 2, 4, 8};
    heapify(data, NUM);
    for(int i=0; i < NUM; i++) {
    
        printf("%d ", data[i]);
    }
    heap_sort(data, NUM);
    printf("\nAfter sorted !!!\n");
    for(int i=0; i < NUM; i++) {
    
        printf("%d ", data[i]);
    }
    return 0;
}

Complexité temporelle du tas

La structure de la pile d'en haut est facile à comprendre , Le tas est une structure d'arbre binaire , S'il y a des éléments dans le tas actuel $N$- Oui., La complexité temporelle de l'insertion d'un élément dans le tas est $O(log(N))$, Quand il coule , Le nombre d'échanges de données ne doit pas être supérieur à $log(N)$.Si un tableau（Pile）Oui.$N$Éléments, Alors il faut le faire. $N$Une fois, L'élément racine est échangé avec le dernier élément du tas , Et les données coulent , Le nombre d'échanges de données par naufrage ne $log(N)$, Et le nombre de fois que vous changez de distance $log(N)$Plus grand., C'est - à - dire qu'il y a moins d'échanges , La complexité temporelle maximale du tri en tas est donc $O(Nlog(N))$.

File d'attente prioritaire

Une file d'attente est une structure de données FIFO , La file d'attente prioritaire est la file d'attente la plus prioritaire . Si vous utilisez un 0 Un nombre entier de , La priorité des données （ Plus le nombre est petit, plus la priorité est élevée. ） Nous pouvons traiter les données avec un petit tas de racines , Parce que l'élément supérieur d'un petit tas de racines doit être le plus petit d'un tas , Donc à chaque fois popFonctionnement, C'est - à - dire que lorsque vous sortez un élément de la file d'attente, vous pouvez échanger l'élément supérieur avec le dernier élément , Ensuite, les nouveaux éléments du Haut de la pile Opération de naufrageC'est tout., S'il y a un nouvel élément à empiler , Alors il peut maintenant être placé à la fin du tableau ,Et ensuiteFlottantFonctionnement, En fait, cette opération est simple et NaufrageC'est pareil., Même les conditions d'arrêt sont les mêmes , C'est le contraire. ,Naufrage Lorsque le noeud courant est un noeud de feuille ou un élément inférieur à un noeud d'enfant （Pour un petit tas de racines）Arrêtez!Naufrage, L'opération flottante s'arrête lorsque le noeud courant est le noeud racine ou que la valeur du noeud courant est supérieure au noeud parent. . Voici une procédure de fonctionnement spécifique .

Une simple opération décrite ci - dessus .C'est très simple.,Il suffit de le maîtriser.Naufrage Le fonctionnement de ce processus est facile à comprendre , Tout ce qui précède concerne le tas ,Si ça t'aide,Trois compagnies~~~