12. Nonlinear support vector machine and kernel function

Linearly separable : Use a separating hyperplane $\omega \cdot x+b$ Separate the data set completely ;

Nonlinear separability : Separate data sets with a hypersurface .

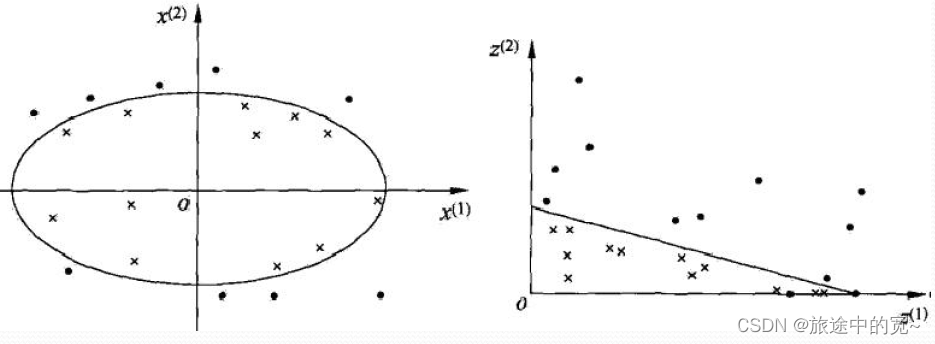
Nonlinear problems are often difficult to solve , So I hope to solve this problem by solving linear classification problems .

The method adopted is to make a nonlinear transformation , Transform nonlinear problems into linear problems , Solve the original nonlinear problem by solving the transformed linear problem .

namely : How to map points in the original space to points in the new space ！

13. What is the use of kernel function ？

The original space : input space $$\begin{array}{rl}& \min \sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,i=1,2,\cdots ,N\end{array}$$

In the upper form $x_i\cdot x_j$ It's an inner product , In the new space, it may become $z$, Corresponding to Hilbert space , Be able to calculate $z_i\cdot z_j$.

Hope to find a mapping $\varphi (x):\chi \to$$H$$$\begin{array}{rl}& z_i=\varphi (x_i),z_j=\varphi (x_j)\\ & z_i\cdot z_j=\varphi (x_i)\cdot \varphi (x_j)=K(x_i,x_j)\end{array}$$

If it can be achieved , Nonlinear support vector machine becomes :
$$\min \sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i$$

Now let's look at an example :

$$K(x,z)=(x\cdot z{)}^2,xz\in R^2$$

Excuse me, :$\varphi \to H$?

Explain : $$x=(x^{(1)},x^{(2)}{)}^T,z=(z^{(1)},z^{(2)}{)}^T$$
$$\begin{array}{rl}K(x,z)& =(x^{(1)}{z}^{(1)}+x^{(2)}{z}^{(2)}{)}^2\\ & =(x^{(1)}{z}^{(1)}{)}^2+2x^{(1)}{x}^{(2)}{z}^{(1)}{z}^{(2)}+(x^{(2)}{z}^{(2)}{)}^2\end{array}$$

We try $H=R^3$
$$\varphi (x)=((x^{(1)}{)}^2,\sqrt{2}{x}^{(1)}{x}^{(2)},(x^{(2)}{)}^2{)}^T$$

1)$\varphi :R^2\to R^3$
$$\varphi (x)\cdot \varphi (z)=(x^{(1)}{z}^{(1)}{)}^2+2x^{(1)}{x}^{(2)}{z}^{(1)}{z}^{(2)}+(x^{(2)}{z}^{(2)}{)}^2=K(x,z)$$

2) $$\begin{array}{rl}& \varphi (x)=\frac{1}{\sqrt{2}}((x^{(1)}{)}^2-(x^{(2)}{)}^2,2x^{(1)}{x}^{(2)},(x^{(1)}{)}^2+(x^{(2)}{)}^2{)}^T\\ & \varphi (x)\cdot \varphi (z)=K(x,z)\end{array}$$

For the same kernel function , There are many different mappings ！

Let's summarize :

The original space : $$\chi \in R^2,x=(x^{(1)},x^{(2)}{)}^T\in \chi$$

New space : $$\begin{array}{rl}& Z\in R^2,z=(z^{(1)},z^{(2)}{)}^T\in Z\\ & z=\varphi (x)=((x^{(1)}{)}^2,(x^{(2)}{)}^2{)}^T\\ \Rightarrow & {\omega }_1(x^{(1)}{)}^2+{\omega }_2(x^{(2)}{)}^2+b=0\\ \Rightarrow & {\omega }_1{z}^{(1)}+{\omega }_2{z}^{(2)}+b=0\end{array}$$

There are two steps to solve the nonlinear classification problem with the linear classification method :

First, a transformation is used to map the data from the original space to the new space ;

Then in the new space, the linear classification learning method is used to learn the classification model from the training data .

Nuclear techniques belong to such methods .

Application of kernel technique to support vector machine , Its basic idea :

The input space is transformed by a nonlinear transformation ( Euclidean space R” Or discrete set ) Corresponding to a feature space ( Hilbert space ), Make the hypersurface model in the input space correspond to the hyperplane model in the feature space ( Support vector machine ). The learning task of classification problem is to solve the linear branch in the feature space
With vector machine, you can complete .

14. How to find a positive definite nucleus

primary :$x_i\cdot x_j$

new :$\varphi (x_i)\cdot \varphi (x_j)=K(x_i,x_j)$ Kernel function

We want to replace the original inner product definition , The inner product of the same vector must be greater than or equal to 0, So finding a positive definite nucleus is the most appropriate .

Explain : First step : We want to find symmetric functions $K(x,z)$

$x,z\in \chi$, For input space .

Need to be right $\forall x_1,x_2,\cdots ,x_m\in \chi$,$K(x,z)$ Corresponding $Gram$ Matrix positive semidefinite .

Why choose at will ？ Because the training data set is uncertain .

our $Gram$ The matrix of the :

The original : $$\left[\begin{array}{cccc}{x}_1\cdot x_1& x_1\cdot x_2& \cdots & x_1\cdot x_m\\ x_2\cdot x_1& x_2\cdot x_2& \cdots & x_2\cdot x_m\\ \cdots & \cdots & \cdots & \cdots \\ x_m\cdot x_1& x_m\cdot x_2& \cdots & x_m\cdot x_m\end{array}\right]$$

new : $$\left[\begin{array}{cccc}K(x_1\cdot x_1)& K(x_1\cdot x_2)& \cdots & K(x_1\cdot x_m)\\ K(x_2\cdot x_1)& K(x_2\cdot x_2)& \cdots & K(x_2\cdot x_m)\\ \cdots & \cdots & \cdots & \cdots \\ K(x_m\cdot x_1)& K(x_m\cdot x_2)& \cdots & K(x_m\cdot x_m)\end{array}\right]$$

Our new matrix needs to satisfy positive semidefinite .

Definition of positive semidefinite : About matrix $A$, Yes $\forall x$（ Nonzero ） There is ,$x^{T}Ax\ge 0$, It's called matrix $A$ It's positive semidefinite .

Definition of seminegative definite :$x^{T}Ax\le 0$

The definition of positive definite :$x^{T}Ax>0$

The definition of negative definite :$x^{T}Ax<0$

Our judgment method is as follows :

The first method : $$x^{T}Ax=y^{T}Dy\ge 0$$

among $D$ It's a diagonal matrix , All elements are greater than or equal to 0.

look for $A$ The characteristic root of the , All are greater than or equal to 0

The second method :

All primary and secondary determinants are greater than or equal to 0

15. New space under mapping

Let's review the previous definition of European space :

Our original space is called vector space or linear space , This space is characterized by addition （+） And number multiplication （$\times$） It's closed .

On this basis, we define the definition of inner product , Make the addition operation （+）、 Number multiplication （$\times$） And inner product operation （$\cdot$） It's closed . Form inner product space .

If we want to know the length of the vector , We introduce the definition of norm , Form normed linear space .

The vector space above 、 Inner product space 、 Normed linear space constitutes our common European space .

further , Want to study convergence and limit , All points are in space , be called $Banach$ Space .

If we didn't study the above content in the well-known Euclidean space , We changed a space , New inner products and norms are defined , And the space is complete , Called Hilbert space .

Specific implementation steps :

Explain : 1):

Form vector space （ Find the vector space ）

$\varphi$ Expressed as :$x\to K(\cdot ,x)$

about $\forall x_i\in \chi ,{\alpha }_i\in R,i=1,2,\cdots ,m$

Definition : $$f(\cdot )=\sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)$$

$f$ Make up a set $S$,$S$ Become a vector space .

verification : from $S$ in $\forall f,g$, Yes : $$\begin{array}{rl}& f=\sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)\\ & g=\sum _{j=1}^v{\beta }_{j}K(\cdot ,z_j)\end{array}$$$$\begin{array}{rl}f+g& =\sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)+\sum _{j=1}^v{\beta }_{j}K(\cdot ,z_j)\\ & =\sum _{i=1}^{m+l}{a}_{i}K(\cdot ,{\mu }_i)\in S\\ af& =\sum _{i=1}^{m}a{\alpha }_{i}K(\cdot ,x_i),a{\alpha }_i\in R\end{array}$$

in summary ,$S$ It is closed to addition and multiplication .

2） In collection $S$ Define inner product on （ Inner product space ）

Definition $\ast$, Yes $\forall f,g\in S$, We define :
$$f\ast g=\sum _{i=1}^m\sum _{j=1}^l{\alpha }_i{\beta }_{j}K(x_i,z_j)$$

The inner product must satisfy four conditions : $$\{\begin{array}{rl}& (1):(cf)\ast g=c(f\ast g),c\in R\\ & (2):(f+g)\ast h=f\ast h+g\ast h,h\in S\\ & (3):f\ast g=g\ast f\\ & (4):f\ast f\ge 0;f\ast f=0\Rightarrow f=0\end{array}$$

Let's next verify whether four conditions are met :

The first is the first : $$\begin{array}{rl}left:& cf=c\sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)=\sum _{i=1}^{m}c{\alpha }_{i}K(\cdot ,x_i)\\ (cf)\ast g& =\sum _{i=1}^m\sum _{j=1}^l(c{\alpha }_i){\beta }_{j}K(x_i,z_j)\\ & =c\sum _{i=1}^m\sum _{j=1}^l{\alpha }_i{\beta }_{j}K(x_i,z_j)\\ & =c(f\ast g)=right\end{array}$$

Then there is the second :

First we define : $$h=\sum _{q=1}^t{b}_{q}K(\cdot ,v_q)$$

Make $a_i,i=1,2,\cdots ,m+l$ Instead of ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m,{\beta }_1,{\beta }_2,\cdots ,{\beta }_l$.

Make ${\mu }_i,i=1,2,\cdots ,m+l$ Instead of $x_1,x_2,\cdots ,x_m,z_1,z_2,\cdots ,z_l$.
$$\begin{array}{rl}& left:(f+g)\ast h=\sum _{i=1}^{m+l}\sum _{q=1}^t{a}_i{b}_{q}K({\mu }_i,v_q)\\ & right:\sum _{i=1}^m\sum _{q=1}^t{\alpha }_i{b}_{q}K({\alpha }_i,v_q)+\sum _{j=1}^l\sum _{q=1}^t{\beta }_j{b}_{q}K(z_j,v_q)\\ \Rightarrow & left=right\end{array}$$

Let's look at the third : Obviously, it has been established , because ${\alpha }_i$ and ${\beta }_j$ You can exchange ,$K(x_i,z_j)$ It's symmetrical , You can also change positions .

Finally, let's look at the fourth :

Let's start with the first part :$f\ast f\ge 0$
$$f\ast f=\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_{j}K(x_i,x_j)$$

because $K(x_i,z_j)$ It's symmetrical , therefore $Gram$ The matrix is positive semidefinite , Yes $x^{T}Ax\ge 0$.

So there is $f\ast f\ge 0$

Next, let's look at the second part :

First, let's look at the sufficiency , That is, if there is $f=0$. $$\begin{array}{rl}& f=\sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)\to {\alpha }_i=0\\ \Rightarrow & f\ast f=\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_{j}K(x_i,x_j)=0\end{array}$$

The sufficiency is proved ！

Before proving the necessity , Let's prove the next :

problem : $$\forall f,g\in S,(f\ast g{)}^2\le (f\ast f)(g\ast g)$$

Explain : take $\lambda \in R$$$\begin{array}{rl}f+\lambda g\in S& \Rightarrow (f+\lambda g)\ast (f+\lambda g)\ge 0\\ & \Rightarrow f\ast f+2\lambda (f\ast g)+{\lambda }^2(g\ast g)\ge 0\end{array}$$

We might as well change : $$(g\ast g){\lambda }^2+2(f\ast g)\lambda +f\ast f\ge 0$$

Is our above formula very close to the problem of quadratic function , If you want to be greater than 0, Just let the discriminant $\Delta$ Is less than or equal to 0 that will do .

That is, we know : $$\begin{array}{rl}& 4(f\ast g{)}^2-4(g\ast g)(f\ast f)\le 0\\ \Rightarrow & (f\ast g{)}^2\le (f\ast f)(g\ast g)\end{array}$$

thus , Our conclusion is supported by . Next , Let's go back to the original question .
$$f=\sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)$$

because $f,g$ Is arbitrary , Take something special $g$, Make $g=K(\cdot ,x)$$$\begin{array}{rl}& f\ast g=\sum _{i=1}^m{\alpha }_{i}K(x,x_i)\\ & (f\ast g{)}^2=\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_{j}K(x,x_i)K(x,x_j)\\ & f\ast f=\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_{j}K(x_i,x_j)\\ & g\ast g=K(x,x)\\ & (f\ast f)(g\ast g)=\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_{j}K(x_i,x_j)K(x,x)\\ & (f\ast g{)}^2\le (f\ast f)(g\ast g)=0\end{array}$$

Because square $(f\ast g{)}^2\ge 0$, So we can get : $$\begin{array}{rl}& (f\ast g{)}^2=0\\ \Rightarrow & f\ast g=0\Rightarrow \sum _{i=1}^m{\alpha }_{i}K(x,x_i)=0\Rightarrow {\alpha }_i=0\Rightarrow f=0\end{array}$$

in summary ,$\ast$ Represents inner product operation . At this point, our vector space becomes an inner product space .

We define $f$ and $g$ The inner product of is :
$$f\cdot g=\sum _{i=1}^m\sum _{j=1}^l{\alpha }_i{\beta }_{j}K(x_i,z_j)$$

3) In collection S Define norms on , Upgrade Hilbert space

Definition : $$||f||=\sqrt{f\cdot f}$$

At this time, the space is transformed into a normed linear space .

In new space K Characteristics : Regeneration ！ Such as : $$\begin{array}{rl}& f(\cdot )=\sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)\\ & K(\cdot ,x)\cdot f=\sum _{i=1}^m{\alpha }_{i}K(x,x_i)=f(x)\end{array}$$

Another example :$K(\cdot ,x)\cdot K(\cdot ,z)=K(x,z)$

summary : What we do here is how to find a Hilbert space from the original space ！

16. Necessary and sufficient conditions for positive definite kernel function

set up $K:\chi \times \chi \to R$ It's a symmetric function , be $K(x,z)$ The necessary and sufficient condition for a positive definite nucleus is $\forall x_i\in \chi ,i=1,2,\cdots ,m$,$K(x,z)$ Corresponding $Gram$ matrix $K=[K(x_i,x_j){]}_{m\times m}$ It's a positive semidefinite matrix .

Next, let's prove this conclusion :

First, let's look at the sufficiency :

$K$ It's a positive semidefinite matrix , Our mapping is : $$\begin{array}{rl}\varphi :& x\to K(\cdot ,x)\\ & \chi \to H\end{array}$$

$K(\cdot ,x)\cdot K(\cdot ,z)=K(x,z)$ It shows that it is regenerative , So at this time $K(x,z)$ Positive definite kernel .

The need for :

$K(x,z)$ Positive definite kernel , So there is the following mapping : $$\begin{array}{rl}& \chi \to H\\ & x\to \varphi (x),z\to \varphi (z)\end{array}$$

We have :$K(\cdot ,x)\cdot K(\cdot ,z)=K(x,z)$

How to judge a matrix as a positive semidefinite matrix ? $$\begin{array}{rl}& \forall x_1,x_2,\cdots ,x_m\in \chi \\ & \forall c_1,c_2,\cdots ,c_m\in R\\ & c=(c_1,c_2,\cdots ,c_m{)}^T\end{array}$$

$$K=\left[\begin{array}{cccc}K(x_1,x_1)& K(x_1,x_2)& \cdots & K(x_1,x_m)\\ K(x_2,x_1)& K(x_2,x_2)& \cdots & K(x_2,x_m)\\ \cdots & \cdots & \cdots & \cdots \\ K(x_m,x_1)& K(x_m,x_2)& \cdots & K(x_m,x_m)\end{array}\right]$$

If there is : $$c^{T}Kc\ge 0$$ said $K$ Is a positive semidefinite matrix . At this time there is :
$$c^{T}Kc=(c_1,c_2,\cdots ,c_m)\left[\begin{array}{cccc}K(x_1,x_1)& K(x_1,x_2)& \cdots & K(x_1,x_m)\\ K(x_2,x_1)& K(x_2,x_2)& \cdots & K(x_2,x_m)\\ \cdots & \cdots & \cdots & \cdots \\ K(x_m,x_1)& K(x_m,x_2)& \cdots & K(x_m,x_m)\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ \cdots \\ c_m\end{array}\right]$$

Method 1 : We use inner product operation $$(c_1,c_2,\cdots ,c_m)\left[\begin{array}{cccc}\varphi (x_1)\cdot \varphi (x_1)& \varphi (x_1)\cdot \varphi (x_2)& \cdots & \varphi (x_1)\cdot \varphi (x_m)\\ \varphi (x_2)\cdot \varphi (x_1)& \varphi (x_2)\cdot \varphi (x_2)& \cdots & \varphi (x_2)\cdot \varphi (x_m)\\ \cdots & \cdots & \cdots & \cdots \\ \varphi (x_m)\cdot \varphi (x_1)& \varphi (x_m)\cdot \varphi (x_2)& \cdots & \varphi (x_m)\cdot \varphi (x_m)\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ \cdots \\ c_m\end{array}\right]$$$$=(c_1,c_2,\cdots ,c_m)\left[\begin{array}{c}\varphi (x_1)\\ \varphi (x_2)\\ \cdots \\ \varphi (x_m)\end{array}\right][\varphi (x_1),\varphi (x_2),\cdots ,\varphi (x_m)]\left[\begin{array}{c}{c}_1\\ c_2\\ \cdots \\ c_m\end{array}\right]=||\sum _{i=1}^m{c}_i\varphi (x_i)|{|}^2\ge 0$$

Method 2 : Directly express quadratic form $$\begin{array}{rl}\sum _{i,j=1}^m{c}_i{c}_{j}K(x_i,x_j)& =\sum _{i,j=1}^m{c}_i{c}_j\varphi (x_i)\cdot \varphi (x_j)\\ & =\sum _{i=1}^m\sum _{j=1}^m[c_i\varphi (x_i)]\cdot [c_j\varphi (x_j)]\\ & =[c_1\varphi (x_1)+c_2\varphi (x_2)+\cdots +c_m\varphi (x_m)]\cdot [c_1\varphi (x_1)+c_2\varphi (x_2)+\cdots +c_m\varphi (x_m)]\\ & =||\sum _{i=1}^m{c}_i\varphi (x_i)|{|}_2^2\end{array}$$

Equivalent definition of positive definite kernel :

set up $\chi \in R^n,K(x,z)$ Is defined in $\chi \times \chi$ Symmetric functions on , If the $\forall x_i\in \chi ,i=1,2,\cdots ,m$,$K(x,z)$ Corresponding $Gram$ matrix $K=[K(x_i,x_j){]}_{m\times m}$ It's a positive semidefinite matrix , said $K(x,z)$ It's positive .

17. Common kernel functions

: Defined in European space

1） Polynomial kernel function $$K(x,z)=(x\cdot z+1{)}^p$$

The general form is : $$(x\cdot z+c{)}^p$$ among $c$ Is a constant .

Decision function :
$$f(x)=sign(\sum _{i=1}^N{a}_i^{\ast }{y}_i\cdot (x_i\cdot x+1{)}^p+b^{\ast })$$

2） Gaussian kernel $$K(x,z)=exp(-\frac{||x-z|{|}^2}{2{\sigma }^2})$$

Decision function :
$$f(x)=sign(\sum _{i=1}^N{a}_i^{\ast }{y}_{i}exp(-\frac{||x-x_i|{|}^2}{2{\sigma }^2})+b^{\ast })$$
: Defined on discrete data sets

The space corresponding to the string is mapped to the high-dimensional space :
$$[{\varphi }_n(s){]}_{\mu }=\sum _{i,s(i)=\mu }{\lambda }^{(i)}$$

$n$ Represents string length ,$s$ Is string ,$l(i)$ Represents the length of a small string .

Example : A text [’big’,’pig’,’bag’]

The length is 2 The substring of is [’bi’,’bg’,’ig’,’pi’,’pg’,’ba’,’ag’]

The feature space of projection takes $R^7$, Calculate the length :（ The last element position ）-（ The first position ）+1

    bi            bg            ig            pi            pg            ba            ag

big ${\lambda }^2$${\lambda }^3$${\lambda }^2$ 0 0 0 0
pig 0 0 ${\lambda }^2$${\lambda }^2$${\lambda }^3$ 0 0
bag 0 ${\lambda }^3$ 0 0 0 ${\lambda }^2$${\lambda }^2$

We came to the conclusion that : $$K(big,pig)={\lambda }^4,K(big,bag)={\lambda }^6$$

The method of measuring the similarity between two strings can be used — Cosine similarity :
$$\cos \theta =\frac{x\cdot y}{||x||||y||}$$

Compare the similarity between two texts , Such as : $$\begin{array}{rl}& \frac{K(big,pig)}{||K(big,big)||||K(pig,pig)||}\\ =& \frac{{\lambda }^4}{\sqrt{{\lambda }^6+2{\lambda }^4}\sqrt{{\lambda }^6+2{\lambda }^4}}\\ =& \frac{{\lambda }^4}{{\lambda }^6+2{\lambda }^4}=\frac{1}{2+{\lambda }^2}\end{array}$$

2） String kernel function $$[{\varphi }_n(s){]}_{\mu }=\sum _{i,s(i)=\mu }{\lambda }^{(i)}$$

18. summary

Linear support vector machines

[ Linear support vector machines ]{}

Input : Training set $T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$, among ,$x_i\in \chi \in R^n,y_i\in \{-1,+1\}$.

Output : Separating hyperplane and classification decision function

Algorithm :

Given penalty coefficient $c\ge 0$, Construction optimization problem $$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0,0\le {\alpha }_i\le c,i=1,2,\cdots ,N\end{array}$$

Solve the optimization problem , Get the best solution
$${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }{)}^T$$

according to ${\alpha }^{\ast }$ solve $${\omega }^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$$

Pick out the ones that match $0<{\alpha }_i^{\ast }<c$ The point of $(x_j,y_j)$ Calculation :
$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)$$

The separation hyperplane is : $${\omega }^{\ast }\cdot x+b^{\ast }=0$$

The decision function is : $$f(x)=sign({\omega }^{\ast }\cdot x+b^{\ast })$$

Nonlinear support vector machines

[ Nonlinear support vector machines ]

Algorithm :

Given penalty coefficient $c\ge 0$, Construction optimization problem $$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0,0\le {\alpha }_i\le c,i=1,2,\cdots ,N\end{array}$$

Solve the optimization problem , Get the best solution
$${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }{)}^T$$

according to ${\alpha }^{\ast }$ solve
$${\omega }^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(\cdot ,x_i)$$

Pick out the ones that match $0<{\alpha }_i^{\ast }<c$ The point of $(x_j,y_j)$ Calculation :
$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x_j)$$

Decision function : $$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x,x_i)+b^{\ast })$$

among $x$ For new instances .