One 、 Basic knowledge of

1.1 Create or copy a 3D or 2D View

Change the thickness of the track line

2d Graphics --> Attributes --> more

1.2 Create a new satellite

1. Create a new scene , Name it earth2moon

2. Create a satellite , Method ：Insert -- New -- Satellite（orbit wizard）

Two 、 Mission requirements

Launch the satellite from Wenchang launch site , After being ignited on the berthing track , after 5 It takes days to reach the height near the moon 200km Polar orbit circumlunar orbit .

3、 ... and 、 Create a process

【 notes 】 stay Satellite1 Of Properties By configuring Astrogator Conduct track design （ Right click --Properties）

3.1  Get near the moon

Target Sequence The configuration is as follows

(1) launch --Launch

modify Epoch etc. .

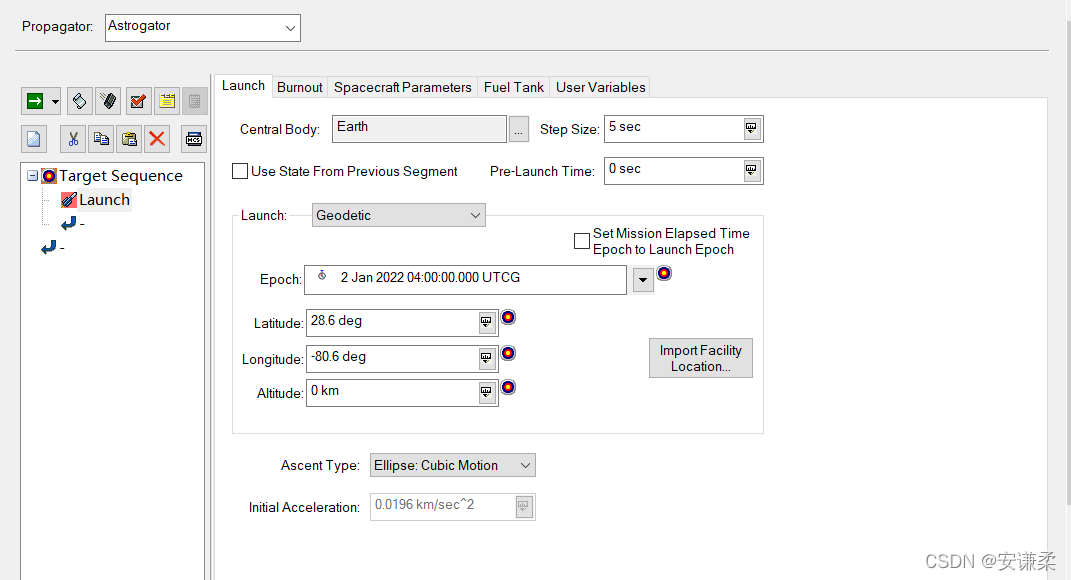
(2) Berthing section --Propagate, Name it Coast

Set the berthing time ：3000 second .

(3) Flying to the moon --Maneuver

Here the thrust uses pulses . Set up , Generally along the direction of speed . perhaps VCN Coordinate system , Along the x Set the axis . Specific values can be found in the literature , Let's see how much it takes for a general lunar orbit , Generally greater than 3000 m/sec.

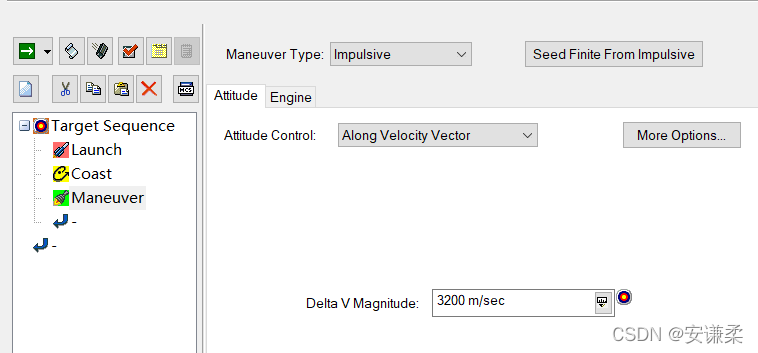
 (4) Propogate

Stop sign 1： Hit the moon and stop . Set the distance from the moon to 0km.

If you can't hit the moon , Stop sign 2： Stop at the point near the moon .

  here , Run the entire sequence , You may find that the moon is not far away , Then it's near the moon , It stopped . however , At this time, it is actually far away from the moon , Still near the earth . In this case, it is impossible to get a feasible solution . therefore , Add a condition （ Set the distance between the satellite and the earth 30000km）, Ensure that the extrapolation is far enough , To the moon .

  Running the whole sequence, I found that there was no rush to the moon . here , We need to change the orientation and position of the space of the lunar orbit . Because it controls the launch time , The orbit to the moon will rotate along the earth's rotation axis . Modify the berthing time , The lunar orbit will rotate along the normal axis of the mooring orbit . therefore , The right ascension of the ascending node needs to be modified by the launch time + Modify the perigee angle according to the berthing time . Check these two design variables . 

  How to describe constraints ？ The satellite's right ascension and declination coincide with the moon . In particular , The target variable is Delta Declination  （Declination between s/c and central body wrt parent body） and Delta Right Asc （Right Ascension between s/c and central body wrt parent body, These two quantities are the difference between the satellite's declination and right ascension relative to the earth and the moon's declination and right ascension relative to the earth .

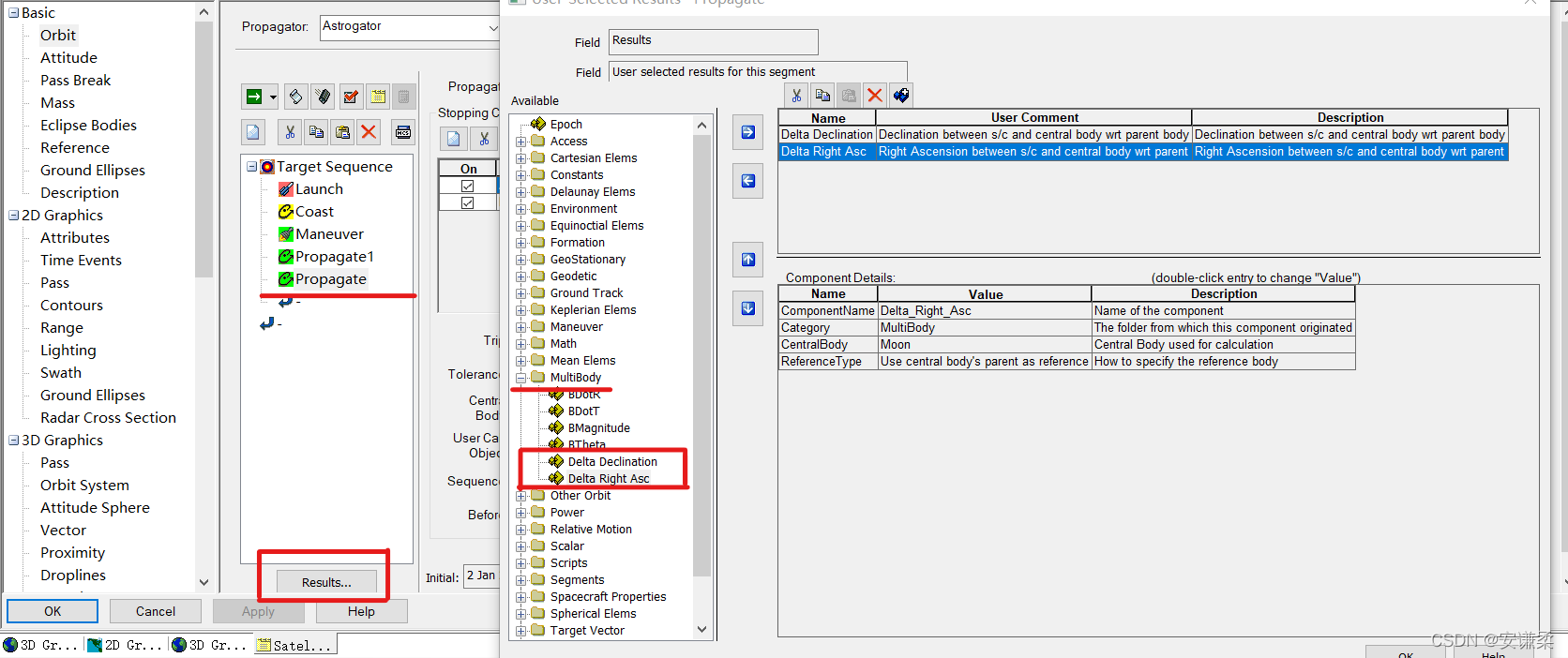
Based on the above analysis , Now let's start configuring the differential solver .(Target Sequence--Differential Corrector)

（1） Design variables （ Control variables ）

 （2） Design objectives

Scaling Is to normalize , Both numerical integral and differential corrections need normalization , It will be easier to solve （ convergence ）.

  Be careful ：Target Sequence Inside Action choice Run active profiles. Click on the run .

give the result as follows

  Come here , The goal of reaching the moon has been achieved .

3.2 Rough design of parameters near the lunar surface

The following is for the height of the perilunar point , dip angle , The flight time is designed .

First , Adjust the inclination .

B Plane is very important in deep space design, especially in the process of gravity assisted orbit transfer . Near small celestial bodies , Relatively small bodies have hyperbolic orbits . The axis passing through the rotation axis and the equator constitute B Plane . The asymptote of hyperbola passes through B The point of the plane is formed by the components of the two axes BDotT and BDotR. The control target of inclination is （Propagate --> Results --> MultiBody） in BDotT and BDotR Definition , It's easier to converge . Because using asymptotes to describe nonlinearity and sensitivity will be much lower .

  here , Add a design variable （ Control variables ）. Pay attention to check .

Suppose the design is a polar orbit of the moon ,BDotR=8000,BDotT=0.

  The specific design of the differential corrector is shown in the figure above , give the result as follows , Convergence is achieved .

then , Adjust the flight time based on the above convergence . The flight time is Propagate --> Results --> Segments --> Difference Across Segments. It literally means to span the deviation between segments . here CalcObject Choice is Epoch,OtherSegment choice Target Sequence.Maneuver.

When I'm done , It can be found that the current flight time is 176727s.

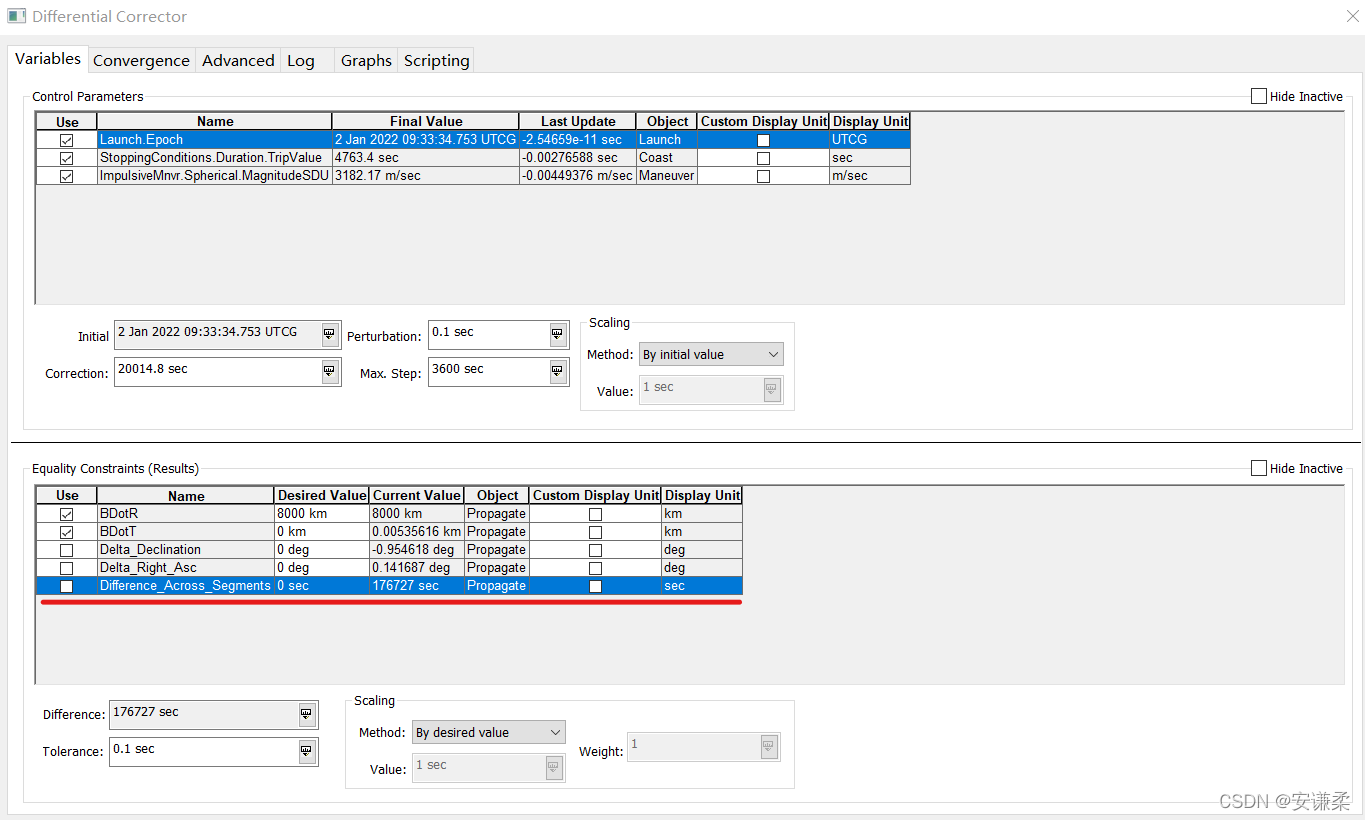If you need to change the time to 5 God , That is to say 432000 second . Copy the above differential corrector , If you modify it directly , See the picture below .

  You will find no convergence ：

  At this time, the homotopy method is used , Gradually change to what you need 432000 Second flight time .

At present, the flight time has met the requirements , The inclination is basically very close to the requirements .

3.3  Precise design of parameters near the lunar surface

Next, the inclination and height are corrected in detail .

The inclination is Propagate --> Results --> Keplerian Elems --> Inclination. The coordinate system is the lunar system .

  The height is at Geodetic --> Altitude, The central celestial body chooses the moon .

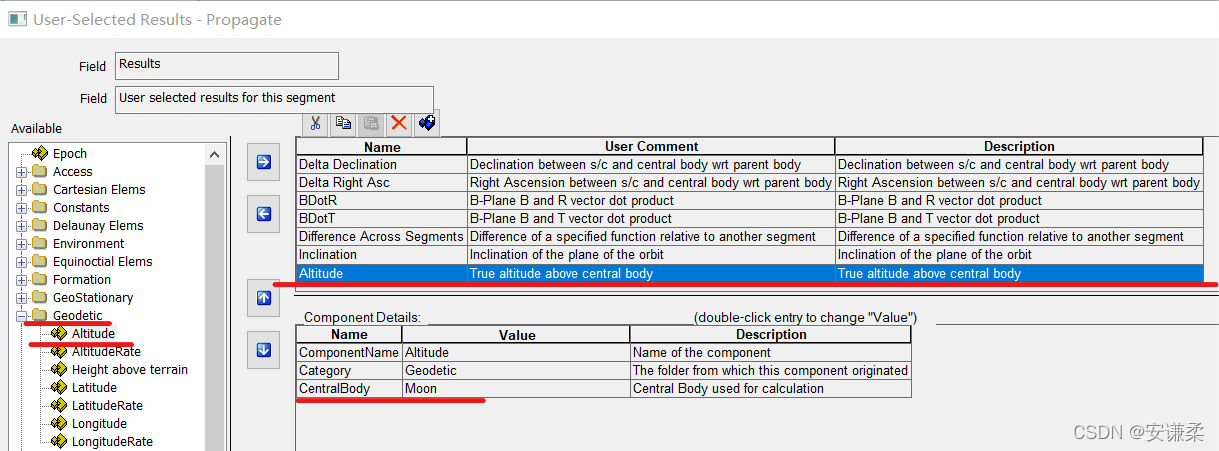
  The constraint is the height of the perilunar point . Why? ？ Because the satellite stopped near the moon （ Extrapolated stop condition ）, So the constraint height means the height of the perihelion . We can see through B After the plane constrains the asymptote , The true inclination of the orbit at this time 83° about , It's close to 90° The requirements of . In this case , It will be easy to converge .

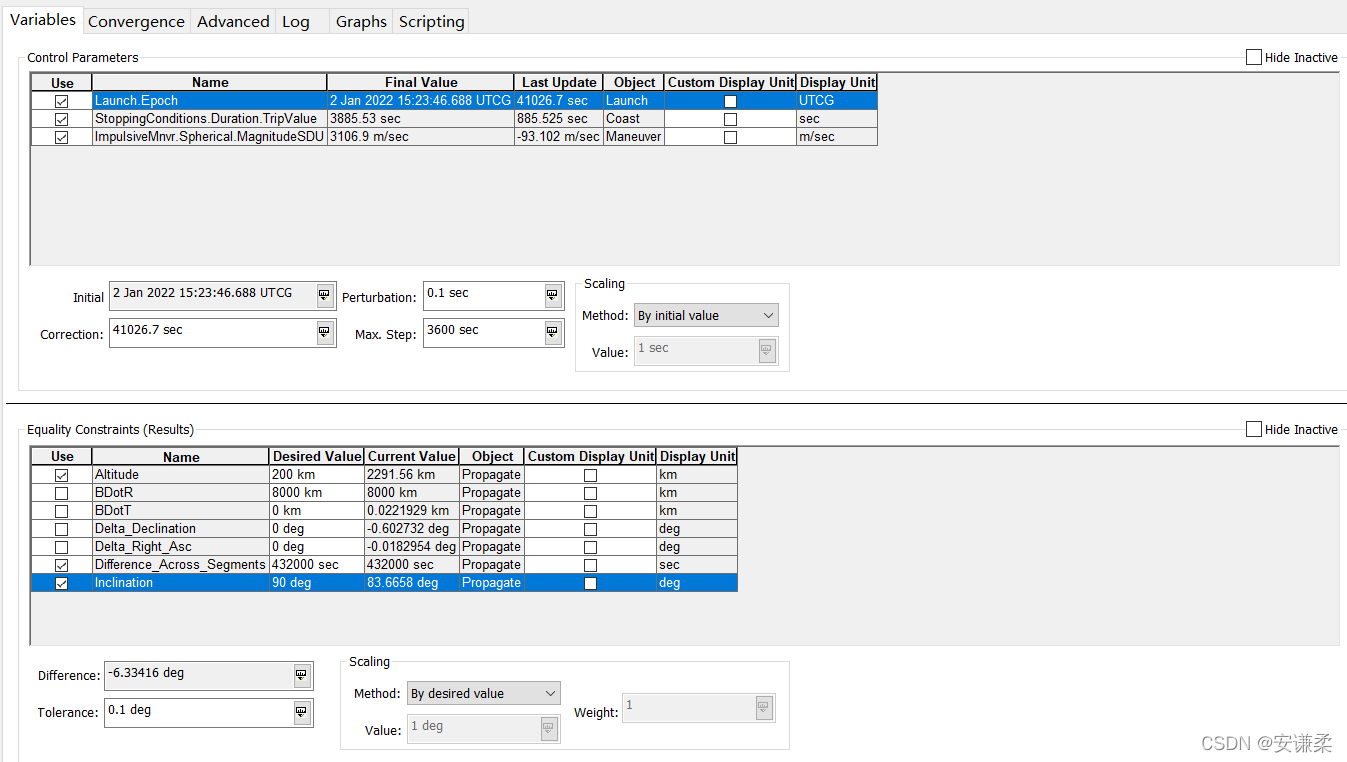
  The operation results are as follows

thus , The design task is completed ！