当前位置：网站首页>Verilog——串行四位加法器和超前四位加法器74HC283

Verilog——串行四位加法器和超前四位加法器74HC283

2022-07-21 16:59:00 【爱学习的岳岳】

一. 串行四位加法器

设计思路

先设计出一位全加器，在根据分层次分模块设计出四位加法器。

1. 一位全加器

1.1原理

根据全加器真值表进行行为级建模。真值表如下图所示：
在这里插入图片描述

1.2代码实现

1.2.1设计模块

module full_adder(
input A,B,Ci,
output reg S,Co);
/*参数说明： 输入： A,B为一位二进制被加数，Ci为来自低位的进位 输出： S为和，Co为进位 */
[email protected](*)
begin
    case({
    A,B,Ci})
	3'b000:begin S=0;Co=0; end
	3'b001:begin S=1;Co=0; end
	3'b010:begin S=1;Co=0; end
	3'b011:begin S=0;Co=1; end
	3'b100:begin S=1;Co=0; end
	3'b101:begin S=0;Co=1; end
	3'b110:begin S=0;Co=1; end
	3'b111:begin S=1;Co=1; end
    endcase
end
endmodule

1.2.2测试模块

//filename:tb_fulladder.v
`timescale 10ns/1ns
module tb_fulladder();
reg A,B,Ci;
wire S,Co;

full_adder U(A,B,Ci,S,Co);

initial
	$monitor($time,"\tA=%b,B=%b,Ci=%b,S=%b,Co=%b",A,B,Ci,S,Co);
initial
begin
	A=0;B=0;Ci=0;
	#5;
	A=1;B=0;Ci=1;
	#5;
	A=1;B=1;Ci=0;
	#5;
	$stop;
end
endmodule

1.3 仿真结果

在这里插入图片描述

2.用四个一位全加器串行成四位加法器

2.1原理

串行进位加法器。采用四个全加器构成四位数加法器。其原理图如图所示，将低位的进位输出信号接到高位的进位输出端。
在这里插入图片描述

2.2代码

2.2.1设计模块

module full_adder(
input A,B,Ci,
output reg S,Co);
/*参数说明： 输入： A,B为一位二进制被加数，Ci为来自低位的进位 输出： S为和，Co为进位 */
[email protected](*)
begin
    case({
    A,B,Ci})
	3'b000:begin S=0;Co=0; end
	3'b001:begin S=1;Co=0; end
	3'b010:begin S=1;Co=0; end
	3'b011:begin S=0;Co=1; end
	3'b100:begin S=1;Co=0; end
	3'b101:begin S=0;Co=1; end
	3'b110:begin S=0;Co=1; end
	3'b111:begin S=1;Co=1; end
    endcase
end
endmodule

module _4adder(
input [3:0] A,B,
input Ci,
output [3:0] S,
output Co);
/*参数说明： 输入： A,B为四位二进制被加数，Ci为来自低位的进位 输出： S为和，Co为进位 */

wire C0,C1,C2;
full_adder U0(A[0],B[0],Ci,S[0],C0);
full_adder U1(A[1],B[1],C0,S[1],C1);
full_adder U2(A[2],B[2],C1,S[2],C2);
full_adder U3(A[3],B[3],C2,S[3],Co);

endmodule

2.2.2测试模块

//filename:tb_4adder.v
`timescale 10ns/1ns
module tb_74HC283();
reg [3:0] A,B;
reg Ci;
wire [3:0] S;
wire Co;
/*参数说明： 输入： A,B为一位二进制被加数，Ci为来自低位的进位 输出： S为和，Co为进位 */

_74HC283 U(A,B,Ci,S,Co);

initial
	$monitor($time,"\tA=%b,B=%b,Ci=%b,S=%b,Co=%b",A,B,Ci,S,Co);
initial
begin
	A=4'b0000;B=4'b0000;Ci=0;
	#5;
	A=4'b0000;B=4'b0000;Ci=1;
	#5;
	A=4'b1111;B=4'b1111;Ci=0;
	#5;
	A=4'b1111;B=4'b1111;Ci=1;
	#5;
	$stop;
end
endmodule

2.3仿真结果

在这里插入图片描述

二.超前四位加法器74HC283

设计思路

行为级建模加法器的功能明晰的，直接列真值表行为级建模，但是在编写过程中发现会出现这样

case({
    A,B,Ci})
	9'b0000_0000_0:begin S=4'b0000;Co=0; end
	9'b0000_0001—0:begin S=4'b0001;Co=0; end
......
    endcase

case语句会出现512条语句，显然不可取。

数据流建模：
由于串行进位加法器速度受到进位信号的限制。人们又设计出一种多位数超前进位加法逻辑电路。
定义两个中间变量：产生变量Gi，传输变量Pi。这两个变量都与进位信号无关。通过代换将各位进位信号表达为只含有Gi，Pi与Ci-1的逻辑表达式（如下），所以个位的进位信号都只与两个加数和向最低位的进位信号Ci-1有关，因此它们是可以并行产生的。
难点核心体现在这个超前进位产生电路中，上面我们知道超前进位产生电路输入和输出的逻辑表达式之后，采用数据流建模即可。
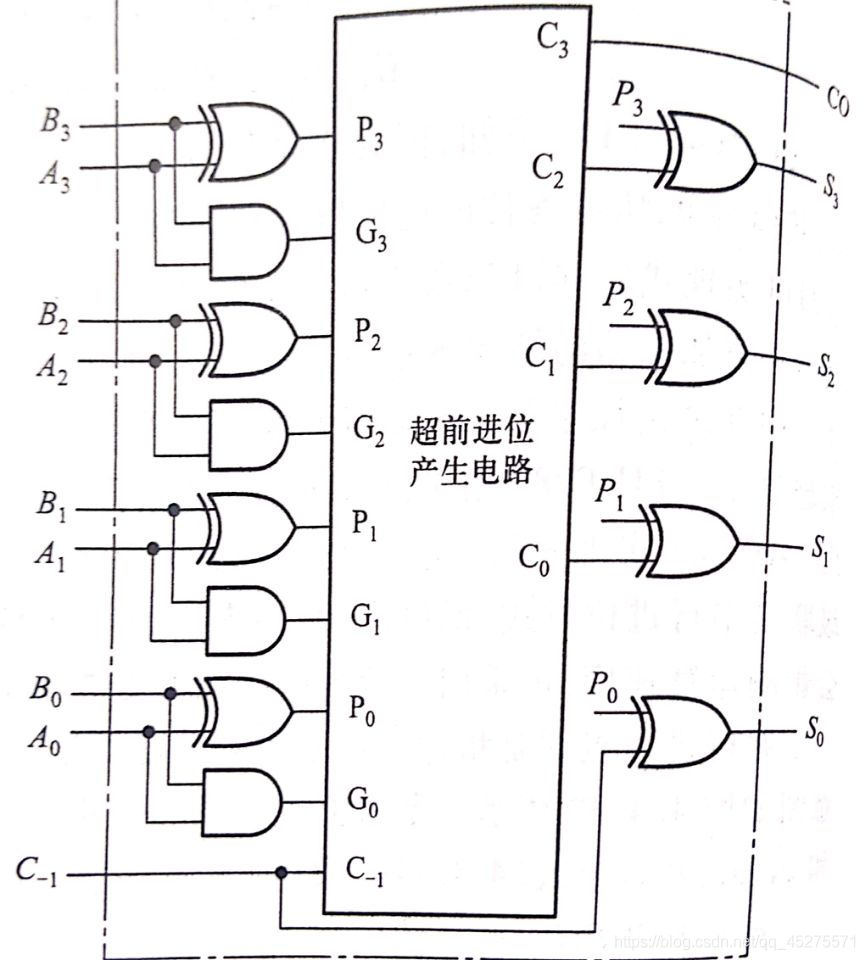
在这里插入图片描述

1.超前进位产生电路

1.1代码实现

1.1.1设计代码

  //filename:ahead_gene_circuit.v
module ahead_gene_circuit(
input [3:0] P,G,
input Ci,
output  [3:0] C);
/*参数说明： 输入： P,G为定义的中间变量，产生变量Gi，传输变量Pi Ci为来自低位的进位 输出： C为各位的进位信号 */
//根据各位进位信号的逻辑表达式，进行数据流建模。
assign C[0]=G[0]|(P[0]&Ci);
assign C[1]=G[1]|(P[1]&C[0]);
assign C[2]=G[2]|(P[2]&C[1]);
assign C[3]=G[3]|(P[3]&C[2]);
endmodule

1.1.2测试代码

//filename:tb_ahead_gene_circuit.v
`timescale 10ns/1ns
module tb_ahead_gene_circuit();
reg [3:0] P,G;
reg Ci;
wire  [3:0] C;

ahead_gene_circuit U(P,G,Ci,C);
initial
	$monitor($time,"\tP=%b,G=%b,Ci=%b,C=%b",P,G,Ci,C);
initial    begin
	P=4'b0000;G=4'b0000;Ci=0;
	#5;
	P=4'b1111;G=4'b1111;Ci=0;
	#5;
	P=4'b1010;G=4'b1010;Ci=0;
	#5;
	P=4'b1010;G=4'b1010;Ci=1;
	#5;
	$stop;
end
endmodule

1.2 仿真结果

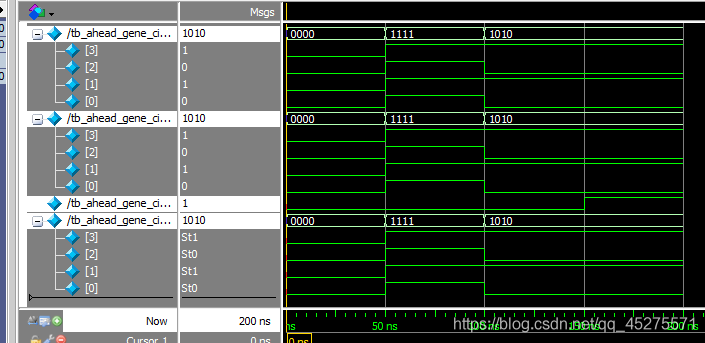
在这里插入图片描述

2.应用超前进位产生电路设计出74HC283

2.1代码实现

2.1.1设计模块

//filename:ahead_gene_circuit.v
module ahead_gene_circuit(
input [3:0] P,G,
input Ci,
output  [3:0] C);
/*参数说明： 输入： Pi为传输信号，Gi为产生信号 Ci为对最低位的进位 输出： C为各位的进位信号 */
//根据各位进位信号的逻辑表达式，进行数据流建模。
assign C[0]=G[0]|(P[0]&Ci);
assign C[1]=G[1]|(P[1]&C[0]);
assign C[2]=G[2]|(P[2]&C[1]);
assign C[3]=G[3]|(P[3]&C[2]);
endmodule

module _74HC283(
input [3:0] A,B,
input Ci,
output [3:0] S,
output Co);
/*参数说明： 输入：A,B为被加数；Ci为对最低位的进位 输出：S为和，co为产生的进位信号 */
//根据中间变量的定义表示出gi和pi。
wire [3:0] P,G,C;
assign P=A^B;
assign G=A&B;
//应用超前进位产生电路。
ahead_gene_circuit U(P,G,Ci,C);

assign Co=C[3];
assign S[3]=C[2]^P[3];
assign S[2]=C[1]^P[2];
assign S[1]=C[0]^P[1];
assign S[0]=Ci^P[0];
endmodule

2.1.2测试模块

`timescale 10ns/1ns
module tb2_74HC283();
reg [3:0] A,B;
reg Ci;
wire [3:0] S;
wire Co;

_74HC283 U(A,B,Ci,S,Co);
initial
	$monitor($time,"\tA=%b,B=%b,Ci=%b,S=%b,Co=%b",A,B,Ci,S,Co);
initial    begin
	A=4'b0000;B=4'b0000;Ci=0;
	#5;
	A=4'b1111;B=4'b1111;Ci=0;
	#5;
	A=4'b1010;B=4'b1010;Ci=0;
	#5;
	A=4'b1010;B=4'b1010;Ci=1;
	#5;
	$stop;
end
endmodule