当前位置:网站首页>洛谷P1955 程序自动分析
洛谷P1955 程序自动分析
2022-07-19 23:12:00 【CLH_W】
题目描述
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设 x_1,x_2,x_3,\cdotsx1,x2,x3,⋯ 代表程序中出现的变量,给定 nn 个形如 x_i=x_jxi=xj 或 x_i\neq x_jxi=xj 的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。例如,一个问题中的约束条件为:x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1x1=x2,x2=x3,x3=x4,x4=x1,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
输入格式
输入的第一行包含一个正整数 tt,表示需要判定的问题个数。注意这些问题之间是相互独立的。
对于每个问题,包含若干行:
第一行包含一个正整数 nn,表示该问题中需要被满足的约束条件个数。接下来 nn 行,每行包括三个整数 i,j,ei,j,e,描述一个相等/不等的约束条件,相邻整数之间用单个空格隔开。若 e=1e=1,则该约束条件为 x_i=x_jxi=xj。若e=0e=0,则该约束条件为 x_i\neq x_jxi=xj。
输出格式
输出包括 tt 行。
输出文件的第 kk 行输出一个字符串 YES 或者 NO(字母全部大写),YES 表示输入中的第 kk 个问题判定为可以被满足,NO 表示不可被满足。
输入输出样例
输入 #1复制
2 2 1 2 1 1 2 0 2 1 2 1 2 1 1
输出 #1复制
NO YES
输入 #2复制
2 3 1 2 1 2 3 1 3 1 1 4 1 2 1 2 3 1 3 4 1 1 4 0
输出 #2复制
YES NO
说明/提示
【样例解释1】
在第一个问题中,约束条件为:x_1=x_2,x_1\neq x_2x1=x2,x1=x2。这两个约束条件互相矛盾,因此不可被同时满足。
在第二个问题中,约束条件为:x_1=x_2,x_1 = x_2x1=x2,x1=x2。这两个约束条件是等价的,可以被同时满足。
【样例说明2】
在第一个问题中,约束条件有三个:x_1=x_2,x_2= x_3,x_3=x_1x1=x2,x2=x3,x3=x1。只需赋值使得 x_1=x_2=x_3x1=x2=x3,即可同时满足所有的约束条件。
在第二个问题中,约束条件有四个:x_1=x_2,x_2= x_3,x_3=x_4,x_4\neq x_1x1=x2,x2=x3,x3=x4,x4=x1。由前三个约束条件可以推出 x_1=x_2=x_3=x_4x1=x2=x3=x4,然而最后一个约束条件却要求 x_1\neq x_4x1=x4,因此不可被满足。
【数据范围】

注:实际上 n\le 10^6n≤106 。
上代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define re register
#define il inline
#define ll long long
using namespace std;
inline int read(){
int s=0,f=0;char c=getchar();
while(c<'0'||c>'9') f=(c=='-'),c=getchar();
while(c>='0'&&c<='9') s=(s<<3)+(s<<1)+(c^'0'),c=getchar();
return f?-s:s;
}
const int N=1e5+5;
int t,n,pre[N],cnt;
struct no{
int x,y,op;
}a[N];
il bool cmp(no x,no y){return x.op>y.op;}
int book[N<<2],b[N<<2],m;
il void init(){
for(re int i=1;i<=m;++i) pre[i]=i;
}
int find(int x){
return pre[x]==x?x:pre[x]=find(pre[x]);
}
bool fl;
il void lsh(){
sort(book+1,book+cnt+1);
for(re int i=1;i<=cnt;++i)
if(i==1||book[i]!=book[i-1]) b[++m]=book[i];
}
il int query(int x){
return lower_bound(b+1,b+m+1,x)-b;
}
int main(){
t=read();
while(t--){
memset(book,0,sizeof(book));cnt=m=0,fl=1;
n=read();
for(re int i=1;i<=n;++i){
a[i].x=read(),a[i].y=read(),a[i].op=read();
book[++cnt]=a[i].x,book[++cnt]=a[i].y;
}
lsh();
sort(a+1,a+n+1,cmp);
init();
for(re int i=1;i<=n;++i){
int x=query(a[i].x),y=query(a[i].y);
int fx=find(x),fy=find(y);
if(a[i].op==1) pre[fx]=fy;
else if(fx==fy){
puts("NO");fl=0;break;
}
}
if(fl) puts("YES");
}
return 0;
}
边栏推荐
- mysql之select查询篇2
- 网络带宽的单位含义
- 驱动虚拟环境搭建记录
- What is CPU virtualization? Open or close?
- 创未来,享非凡,openGauss Developer Day 2022圆满举行
- 面试题 08.07. 无重复字符串的排列组合-dfs法
- 一篇文章带你快速学会Flex布局
- ECCV 2022 | semantic novelty detection based on relational reasoning
- 【Flink】转换算子 map
- RuntimeError: CUDA error: an illegal memory access was encountered
猜你喜欢

「接口测试入门课」打卡学习 day04:如何把流程化的测试脚本抽象为测试框架?

Chengdu small products in 1998, joined a state-owned enterprise for two and a half years, and the salary exceeded 18K

MySQL表的增删查改(二)
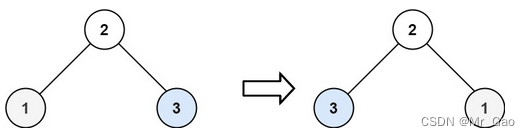
226. 翻转二叉树-dfs法
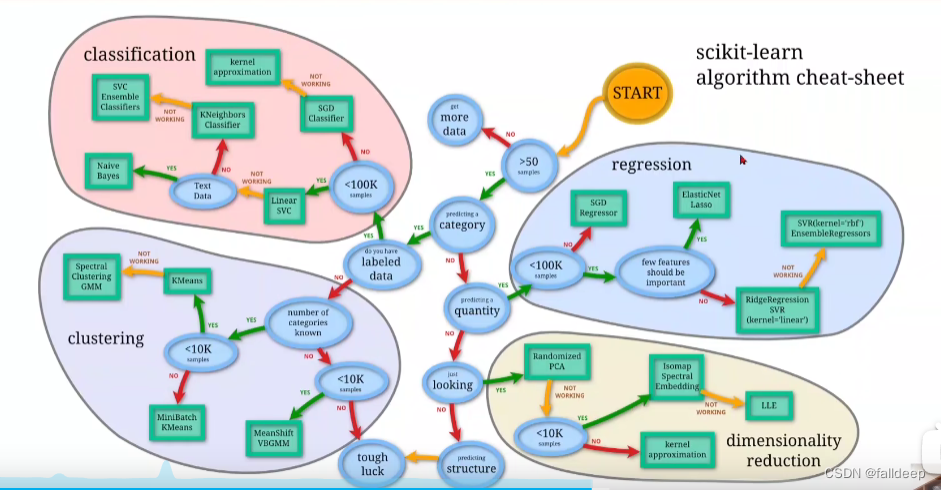
深度学习从零构建一个模型的方法

openGauss社区理事长江大勇:openGauss联合产业界创新,共建开源数据库根社区
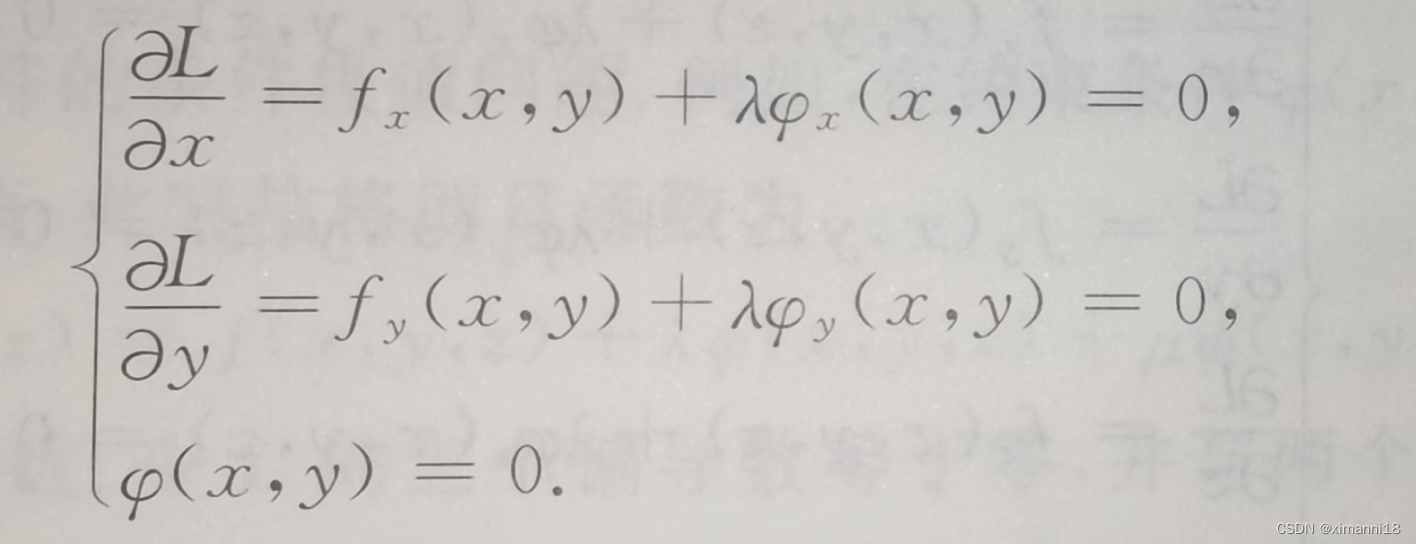
高数_第2章多元函数微分学__求解条件极值的方法__拉格朗日乘数法

【ROS】roslaunch的使用

【ROS】手写消息发布器和订阅器

性能测试学习之jmeter单场景使用示例
随机推荐
数组把key相同值,合并value值(整理)
openvino模型学习-从模型转化流水线制作
浅析IM即时通讯开发之扫码登录二维码
[Axi] interpret the low-power design of Axi protocol
【云原生】 iVX 低代码开发 引入腾讯地图并在线预览
Job hopping After 3 rounds of interviews for byte test post, 4 hours of soul torture, the ending is cool
What is CPU virtualization? Open or close?
【软考软件评测师】2015综合知识历年真题
Cnpm installation
冒泡排序
【MySql 实战】高度聚合的数据项拆分为多行多列
MySQL十九:分库分表实践
Target segmentation for 10000 frames of video, less than 1.4GB of video memory, open source code | ECCV 2022
High number_ Chapter 2 differential calculus of multivariate functions__ Method of solving conditional extremum__ Lagrange multiplier method
These super easy-to-use browser plug-ins are unknown to many people
MySQL5.7 参数详解
mysql之select查询篇2
Camtasia 2022新版本发布CS喀秋莎2022功能亮点
洛谷P5250 木材仓库
几种2022年流行的跨端技术方案的优缺点