当前位置：网站首页>无人机的微分平坦性详细推导

无人机的微分平坦性详细推导

2022-07-21 05:05:00 【什么时候能造钢铁侠啊】

无人机的微分平坦性详细推导

目标：将无人机的状态一个12维的向量用4维表示
即将无人机的位置，方向，速度和角速度用位置(X,Y,Z)和绕z轴的 $\psi$ 角表示
无人机状态矩阵

1.无人机非线性动力学

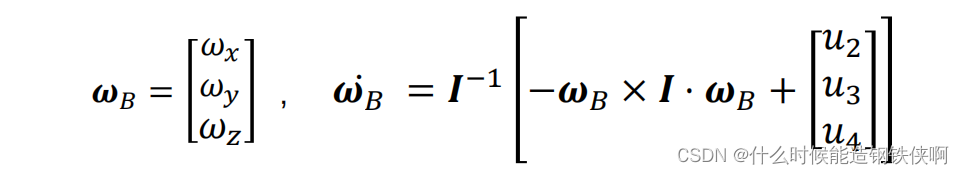
在这里插入图片描述

2.机体坐标系表示

无人机的推力始终与机架垂直因此
$Z_B=\frac{t}{\|t\|}$ , $t=[\ddot x,\ddot y,\ddot z + g]^{\mathbf T}$
然后我们通过一个中间坐标系来求 $Y_B$ ,坐标系如图1的， $X_C，Y_C,Z_C$ 。
$X_C=[cos\psi,sin\psi,0]^{\mathbf T}$
通过 $X_C$ 我们得到 $Y_B$
$Y_B=\frac{Z_B \times X_C}{\|Z_B \times X_C\|}$ (因为 $X_C$ 和 $X_B,Z_B$ 在一个平面内)
$X_B=Y_B \times Z_B$
$R_B=[X_B \ Y_B \ Z_B]$ （它表示的旋转可以由 $\phi,\theta,\psi$ 的旋转矩阵表示，因此这三个角可以被消除掉）

3.角速度替换

对下式两边求导，（对一个旋转矩阵求导，等于它的角速度乘以本身这个坐标系。旋转矩阵求导看这里: 旋转矩阵求导
在这里插入图片描述
$\omega_{BW}=\omega_xX_B+\omega_yY_B+\omega_zZ_B$ 表示体坐标系下的角速度
上式中的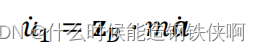

将它带入上式得到

这里的 $h_\omega$ 的所有量都是已知量
$h_\omega=\omega_{BW}\times Z_B=(\omega_xX_B+\omega_yY_B+\omega_zZ_B)\times Z_B$
因为
$X_B\times Z_B=-Y_B$
$Y_B\times Z_B=X_B$
$Z_B\times Z_B=\overrightarrow{0}$
因此上式可以展开为
$h_\omega= - \omega _x \times Y_B+\omega _y\times X_B$
然后两边点乘 $Y_B$ ,得到
$\omega _x=-h_\omega \cdot Y_B$
两边点乘 $X_B$ ,得到
$\omega _Y=h_\omega \cdot X_B$
因为 $\omega_{BW}=\omega _{BC}+\omega _{CW}$ ,而 $\omega _{BC}$ 在 $Z_B$ 上没有分量，
因此 $\omega _z=\omega _{BW}\cdot Z_B=\omega _{CW} \cdots Z_B=\dot \psi Z_W \cdot Z_B$
至此12维变量变成了4维变量表示。
在实际的路径规划中我们只需要规划出轨迹的位置， $\psi$ 角通常表示为速度的切向方向（群里咨询的，不知是否还有什么知识不知道）。具体的控制回路如下；
例如在mini snap规划时我们只需要将规划的轨迹加上速度的切线方向丢这个控制回路，就可以实现无人机的飞行。