The differential flatness of UAV is derived in detail

The goal is ： Turn the status of the UAV into 12 The vector of dimension is 4 Wei said
About the location of the drone , Direction , Velocity and angular velocity are used for position (X,Y,Z) And around z The shaft $\psi$ Angular representation

1. UAV nonlinear dynamics

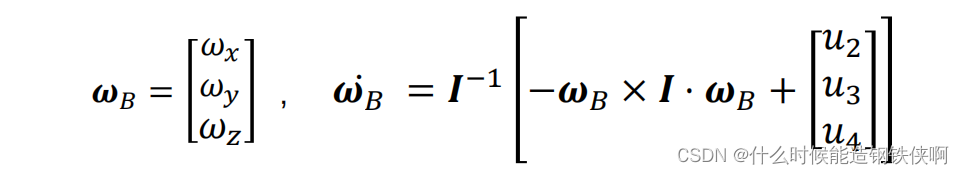
2. The body coordinate system represents

The thrust of the UAV is always perpendicular to the frame, so
$Z_B=\frac{t}{\Vert t\Vert }$,$t=[\ddot{x},\ddot{y},\ddot{z}+g{]}^{\mathbf{T}}$
Then we use an intermediate coordinate system to find $Y_B$, The coordinate system is shown in the figure 1 Of ,$X_C,Y_C,Z_C$.
$X_C=[cos\psi ,sin\psi ,0{]}^{\mathbf{T}}$
adopt $X_C$ We get $Y_B$
$Y_B=\frac{Z_B\times X_C}{\Vert Z_B\times X_C\Vert }$( because $X_C$ and $X_B,Z_B$ In a plane )
$X_B=Y_B\times Z_B$
$R_B=[X_B{Y}_B{Z}_B]$（ The rotation it represents can be represented by $\varphi ,\theta ,\psi$ The rotation matrix of , So these three corners can be eliminated ）

3. Angular velocity replacement

Take the derivative on both sides of the following formula ,（ Take the derivative of a rotation matrix , Equal to its angular velocity times its own coordinate system . Derivative of rotation matrix see here : Derivation of rotation matrix

${\omega }_{BW}={\omega }_x{X}_B+{\omega }_y{Y}_B+{\omega }_z{Z}_B$ Represents the angular velocity in the volume coordinate system
On the type of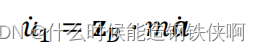

Bring it into the above formula to get

there $h_{\omega }$ All quantities of are known
$h_{\omega }={\omega }_{BW}\times Z_B=({\omega }_x{X}_B+{\omega }_y{Y}_B+{\omega }_z{Z}_B)\times Z_B$
because
$X_B\times Z_B=-Y_B$
$Y_B\times Z_B=X_B$
$Z_B\times Z_B=\overrightarrow{0}$
Therefore, the above formula can be expanded into
$h_{\omega }=-{\omega }_x\times Y_B+{\omega }_y\times X_B$
And then on both sides Point multiplication $Y_B$, obtain
${\omega }_x=-h_{\omega }\cdot Y_B$
Both sides Point multiplication $X_B$, obtain
${\omega }_Y=h_{\omega }\cdot X_B$
because ${\omega }_{BW}={\omega }_{BC}+{\omega }_{CW}$, and ${\omega }_{BC}$ stay $Z_B$ There is no weight on ,
therefore ${\omega }_z={\omega }_{BW}\cdot Z_B={\omega }_{CW}\cdots Z_B=\dot{\psi }{Z}_W\cdot Z_B$
thus 12 Dimensional variables become 4 Dimensional variables represent .
In the actual path planning, we only need to plan the location of the trajectory ,$\psi$ The angle is usually expressed as the tangential direction of velocity （ Consulted in the Group , I wonder if there is any knowledge I don't know ）. The specific control circuit is as follows ;
For example, in mini snap When planning, we only need to throw the planned trajectory plus the tangent direction of speed into this control loop , Can realize the flight of UAV .

— Refer to the mobile robot path planning course of Deep Blue College