当前位置:网站首页>Force deduction record: dynamic programming 5 Subsequence Problems (2) editing distance - 392 judging subsequences, 115 different subsequences, 583 deleting operations of two strings, 72 editing dista
Force deduction record: dynamic programming 5 Subsequence Problems (2) editing distance - 392 judging subsequences, 115 different subsequences, 583 deleting operations of two strings, 72 editing dista
2022-07-21 22:48:00 【Kiwi_ fruit】
This topic
- 392 Judging subsequences
- 115 Different subsequences
- 583 Deletion of two strings
- 72 Edit distance
392 Judging subsequences
- DP:
- Definition dp Array dp[i][j] Indicates subscript i-1( Include i-1) Previous string s And subscripts j-1( Include j-1) Previous string t, The same subsequence length is dp[i][j];
- Recurrence formula if s[i - 1] == t[j - 1], be dp[i][j] = dp[i - 1][j - 1] + 1, otherwise dp[i][j] = dp[i][j - 1];
- initialization dp[0][j] and dp[i][0] by 0;
- Ergodic order positive order ;
- give an example .
class Solution {
public boolean isSubsequence(String s, String t) {
//DP
int s_leng = s.length();
int t_leng = t.length();
// Judge special cases
// if(s_leng == 0) return true;
// if(s_leng != 0 && t_leng == 0) return false;
// if(s_leng > t_leng) return false;
// Definition dp Array dp[i][j] Indicates subscript i-1( Include i-1) Previous string s
// And subscripts j-1( Include j-1) Previous string t, The same subsequence length is dp[i][j]
int[][] dp = new int[s_leng + 1][t_leng + 1];
// initialization dp[0][j] and dp[i][0] by 0
// Ergodic order positive order
for(int i = 1; i <= s_leng; i++){
for(int j = 1; j <= t_leng; j++){
if(s.charAt(i - 1) == t.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = dp[i][j - 1];
}
// if(dp[i][j] == s_leng) return true;
}
}
if(dp[s_leng][t_leng] == s_leng) return true;
// Finally back to false
return false;
}
}
115 Different subsequences
- DP:
- Definition dp Array dp[i][j] Indicates subscript i-1( Include i-1) Previous s Subscripts appear in subsequences j-1 Previous t The number of subsequences is dp[i][j];
- Recurrence formula if s[i - 1] == t[j - 1], be dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j], otherwise dp[i][j] = dp[i - 1][j];
- initialization dp[i][0] = 1,dp[0][j] = 0,dp[0][0] = 1;
- Ergodic order positive order ;
- give an example .
class Solution {
public int numDistinct(String s, String t) {
//DP
int s_leng = s.length();
int t_leng = t.length();
// Judge special cases
if(t_leng == 0) return 1;
if(s_leng == 0) return 0;
// Definition dp Array dp[i][j] Indicates subscript i-1( Include i-1) Previous s In subsequence
// Subscript subscript j-1 Previous t The number of subsequences is dp[i][j]
int[][] dp = new int[s_leng + 1][t_leng + 1];
// initialization dp[i][0] = 1,dp[0][j] = 0,dp[0][0] = 1
for(int i = 0; i <= s_leng; i++){
dp[i][0] = 1;
}
// Ergodic order positive order
for(int i = 1; i <= s_leng; i++){
for(int j = 1; j <= t_leng; j++){
if(s.charAt(i - 1) == t.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}else{
dp[i][j] = dp[i - 1][j];
}
}
}
// Return results
return dp[s_leng][t_leng];
}
}
583 Deletion of two strings
- Compare with the above 115 Different subsequences , Both strings of this question can be deleted .
- DP:
- Definition dp Array dp[i][j] Indicates subscript i-1 Before ( Include i-1) Substring of 1 And subscripts j-1 Before ( Include j-1) The minimum number of times to delete when the substrings of are equal ;
- Recurrence formula if word1[i - 1] == word2[j - 1],dp[i][j] = dp[i - 1][j - 1], otherwise dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1};
- initialization dp[i][0] = i and dp[0][j] = j;
- Ergodic order positive order ;
- give an example .
class Solution {
public int minDistance(String word1, String word2) {
//DP
int leng1 = word1.length();
int leng2 = word2.length();
// Definition dp Array dp[i][j] Indicates subscript i-1 Before ( Include i-1) Substring of 1
// And subscripts j-1 Before ( Include j-1) The minimum number of times to delete when the substrings of are equal
int[][] dp = new int[leng1 + 1][leng2 + 1];
// initialization dp[i][0] = i and dp[0][j] = j
for(int i = 0; i <= leng1; i++){
dp[i][0] = i;
}
for(int j = 0; j <= leng2; j++){
dp[0][j] = j;
}
// Ergodic order positive order
for(int i = 1; i <= leng1; i++){
for(int j = 1; j <= leng2; j++){
if(word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1];
}else{
dp[i][j] = Math.min(dp[i - 1][j] + 1, Math.min(dp[i][j - 1] + 1, dp[i - 1][j - 1] + 2));
}
}
}
// Return results
return dp[leng1][leng2];
}
}
72 Edit distance
- Compare with the previous question 583 Deletion of two strings , This question can not only be deleted , You can also insert and replace , But the overall thinking is the same ( Inserting one string is equivalent to deleting the other string ).
- DP:
- Definition dp Array dp[i][j] Indicates subscript i-1 Before ( Include i-1) String 1 And subscripts j-1 Before ( Include j-1) String 2 The nearest editing distance of is dp[i][j];
- Recurrence formula if word1[i - 1] == word2[j - 1],dp[i][j] = dp[i - 1][j - 1], otherwise dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
- initialization dp[i][0] = i and dp[0][j] = j;
- Ergodic order positive order ;
- give an example .
class Solution {
public int minDistance(String word1, String word2) {
//DP
int leng1 = word1.length();
int leng2 = word2.length();
// Definition dp Array dp[i][j] Indicates subscript i-1 Before ( Include i-1) String 1
// And subscripts j-1 Before ( Include j-1) String 2 The nearest editing distance of is dp[i][j]
int[][] dp = new int[leng1 + 1][leng2 + 1];
// initialization dp[i][0] = i and dp[0][j] = j
for(int i = 0; i <= leng1; i++){
dp[i][0] = i;
}
for(int j = 0; j <= leng2; j++){
dp[0][j] = j;
}
// Ergodic order positive order
for(int i = 1; i <= leng1; i++){
for(int j = 1; j <= leng2; j++){
if(word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1];
}else{
dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
}
}
}
// Return results
return dp[leng1][leng2];
}
}
边栏推荐
猜你喜欢

74. Search two-dimensional matrix

Expression evaluation

226. Flip binary tree

Atcoder beginer contest 218 problem solution

数据库初学笔记

Probability theory - variance and covariance, correlation coefficient

Redis主从复制的配置原理和过程

Cocos Creator 3. X physics engine usage notes

HoloLens读取和下载Json文件问题(个人Hololens2进阶开发小总结二)
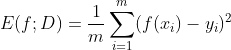
Watermelon book chapter 2 Notes - Performance Measurement
随机推荐
力扣记录:动态规划5子序列问题(1)——300 最长上升子序列,1143 最长公共子序列,1035 不相交的线,674 最长连续递增序列,718 最长重复子数组,53 最大子序和
QT beginner
D - AND and SUM (AtCoder Beginner Contest 238)
第三周ACM训练报告
Quick sort
unity 自定义工具之“执行bat文件”
第五周ACM训练报告
n的阶乘
110. Balanced binary tree
2022acm summer training weekly report (I)
844. Compare strings with backspace
HoloLens读取和下载Json文件问题(个人Hololens2进阶开发小总结二)
寒假学习总结
Cookie quick start
ACM training report of the second week
归并排序
D - AND and SUM (AtCoder Beginner Contest 238)
一个好用的Unity Touch管理器
Cocos Creator 3.2 中实现2D地图3D人物45度角RPG游戏效果笔记(摄像机设置方案)
19. Delete the penultimate node of the linked list