当前位置:网站首页>线段树杂谈·普通线段数|乘法线段数|主席树
线段树杂谈·普通线段数|乘法线段数|主席树
2022-07-19 08:43:00 【大千小熊】
首先非常感谢涛涛学长的认可与厚爱,让小熊同学有机会在这里和大家共同探讨线段树的问题。
(。・ω・。)
一点点前置知识x<<1相当于 x ∗ 2 x*2 x∗2,x<<1|1相当于 x ∗ 2 + 1 x*2+1 x∗2+1。
线段数是什么
线段树,“线段”是“树”的修饰词。对于线段树,它首先是一颗树。
顾名思义,它是由线段构成的一颗树。
请看下图:
我们知道线段是有长度的,比如对于(1)号节点,它的长度就是L=1,R=4, L − R + 1 = 4 L-R+1=4 L−R+1=4。同理,对于(2)号节点,它的长度是L=1,R=2, L − R + 1 = 2 L-R+1=2 L−R+1=2。
并且,这个树是一颗二叉树,或者说,是一颗完全二叉树。并且,节点的编号个数,约等于 2 ∗ N 2*N 2∗N。例如上图, N = 4 N=4 N=4,它有7个节点。(嘿,为什么是 4 N 4N 4N,这里请去二叉树复习,简单来说,就是等比数列求和,和log函数,公式如下: 2 l o g 2 ( N ) + 1 − 1 2^{log_2{(N)}+1}-1 2log2(N)+1−1)
问题的引入
朴素的问题
现在,我们有一个数组a = [1, 2, 3, 4]。
然后,我们有这样一类问题,那么就是,对于区间进行Add操作,例如,对于区间1-4进行+2的操作。
按照我们最容易想到的算法是,通过一个For循环,然后对元素一个个遍历,然后发现这个元素就是我们要修改的元素,那么我们就对这个元素执行Add。
这样做法当然没错,而且也很直观,这个算法的复杂度是O(N)。
优化的火花
现在,让我们来想想,在进行区间修改的时候,我们能不能有一种更快的方法,去修改它,使得它的时间复杂度可以往下降一降。
例如,在,每次修改区间的时候,我为什么要求去对元素进行操作,我可不可以创建一个History历史记录,这个记录记录了我是怎么去修改这个区间的,当我要去查询某一个元素的时候,那么就按照History给出的指南,利用原来的a数组,就可以还原出真正的答案。
这种感觉就好像,对于每次修改,我先不做,当查询一个元素的时候,我再做。这样至少,对于修改操作来说,每次的时间复杂度可以为O(1),因为我只要记录进History即可。
这样想已经很棒了,至少我们已经有了一点点的启发。现在让我们来看看查询操作。对于Query每个点,我们需要还原History的操作,这依赖于,History的长度,当用户修改的越多,那么还原的时候也就更累,时间复杂度更复杂。
让我们再次开动脑筋。
没错,那就是,线段树!
优化的再次进化
现在,我们可以认为,线段树就是一个History,还是原来的图片,原来的a数组(在“朴素的问题”那里)。
对于(1)节点,这个节点L和R表示的区间是,1-4,那么当我们在1-4进行Add操作的时候,完全可以把我们的操作记录在这个节点上。
那,当我们对1-3区间进行操作的时候,我们还可以将操作记录在1-4节点上面嘛?
不正确!首先我们明确,(1)节点记录的是在1-4这个整体区间的操作,1-3区间的操作,并不包含着,第4号节点。所以,这是错误的,对于(2)号节点,它代表着区间1-2,1-2包好在1-3之间,所以(2)号节点是可以进行Add操作的。然后就是(6)号节点,进行Add操作。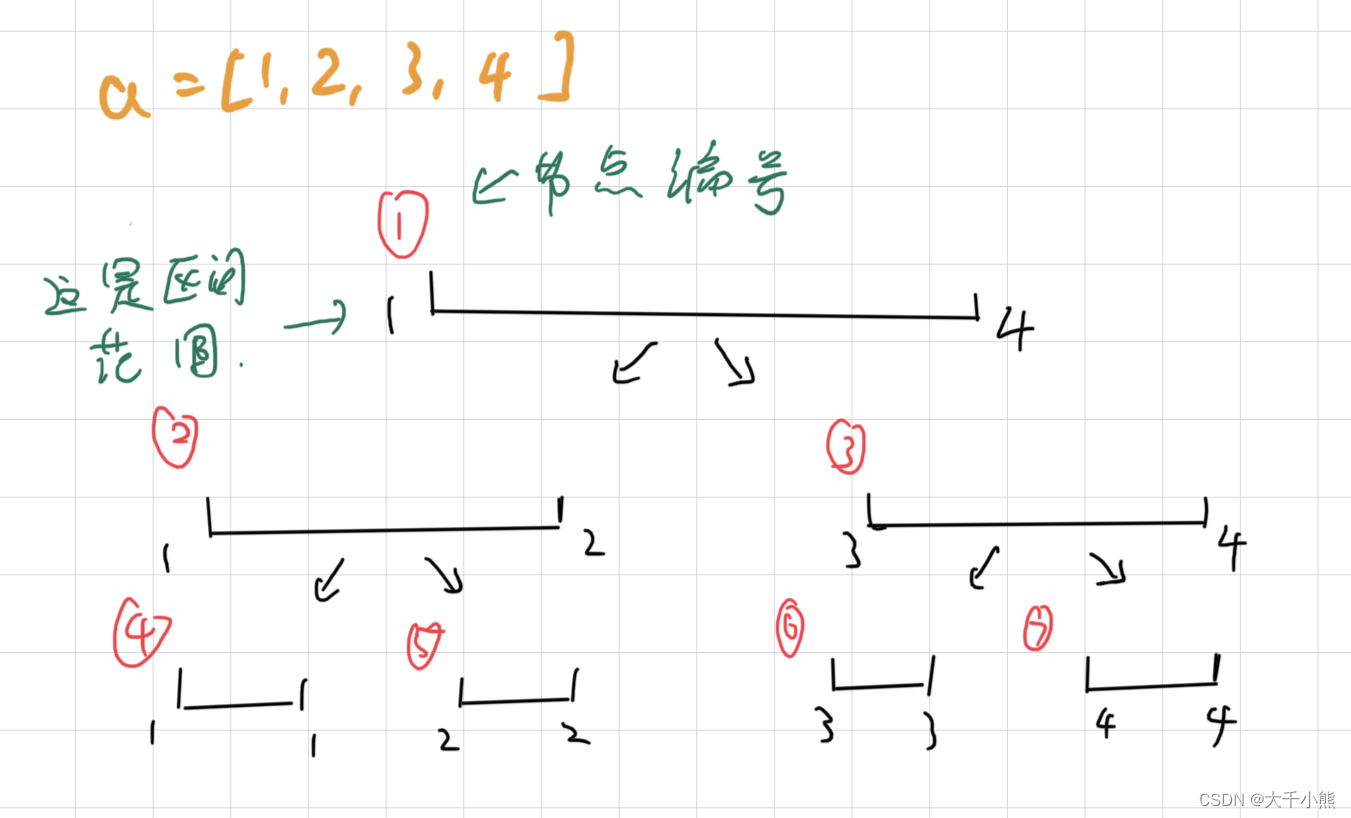
现在,让我们模拟一种情况:
第一次操作:对于区间[1,4] 加2
(我们定义v是对于本节点区间的修改值)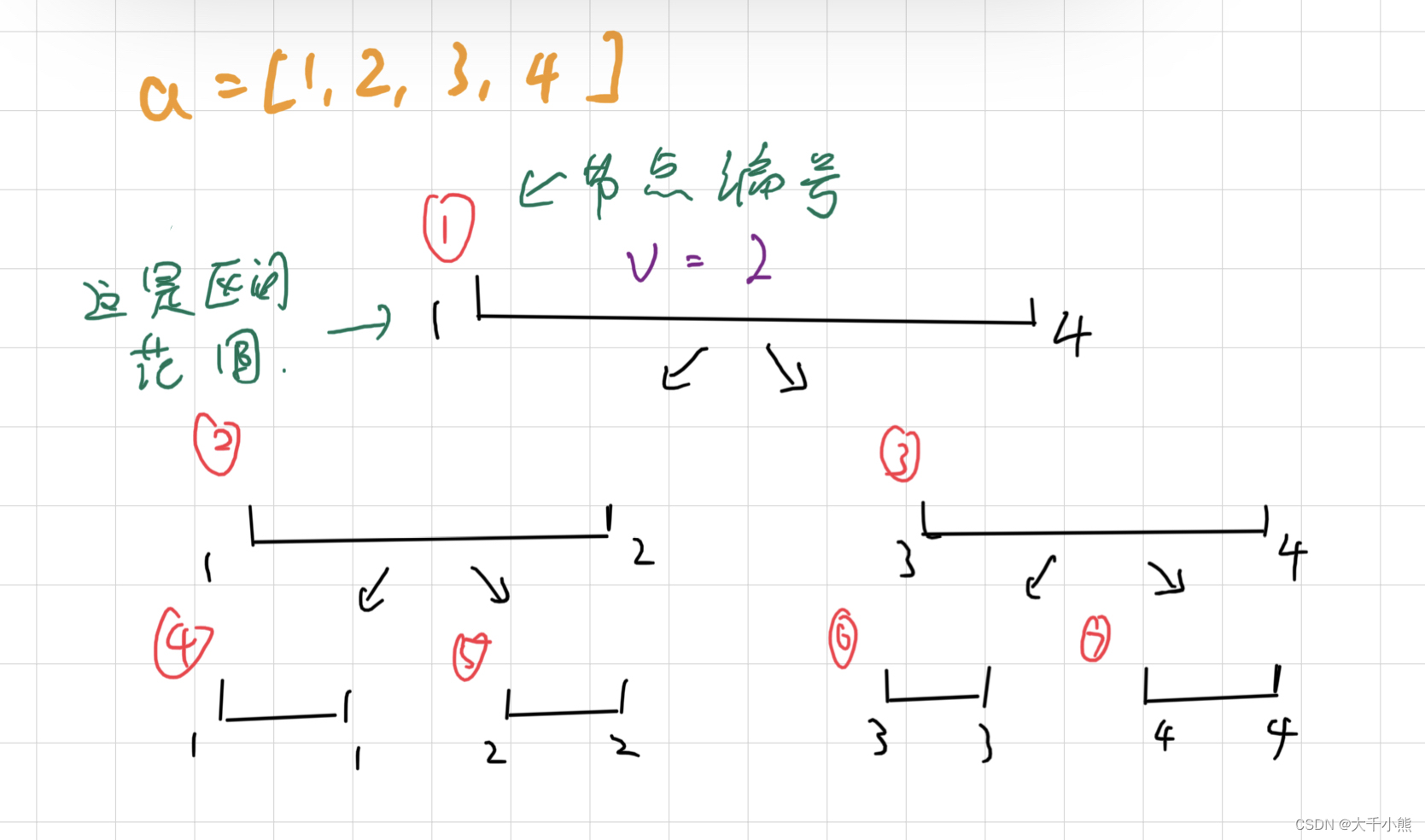
第二次操作:对于区间[1,3] 加1
没错,线段树也可以是一个History。
现在让我们来查询,a[0]再修改后是几,对于a[0],它首先经过线段数(1)号节点的修改,它被加了2,然后对于(2)号节点,它又被加了1,然后到(4)号节点,此时,(4)号节点代表着,区间[1,1],对应a[0]
a[0]除了被(1)、(2)、(4)节点修改以外,不可能再被别点节点修改了。
例如,a[0]不会被(3)号节点修改,因为(3)号节点意味着,历史记录于[3,4]的区间。
所以,我们可以得到,a[0]=a[0]+2+1=4。
线段树是一个历史记录,我们根据线段树,还原了最后修改之后,本点的值。
现在,查询和修改,都是 l o g ( N ) log(N) log(N)级别,回忆一下,二叉查找算法的,复杂度原理。对于每次修改查询,我都根据mid来选择进入左子树或右子树,每次砍一半,当然是log级别的啦。
但是,现在我们又有了一个新的问题:
区间查询怎么办,正如您上面所看到的,我们刚刚的是单点查询,而区间查询的话,我们可能要变为N*log(N),那就是,单独计算需要累加的点,然后加在一起算出区间的值。
我们有没有更好的办法?
当然有了,因为我看过别人的教程了,这篇文章也在CSDN,将在末尾给出。
代码指南(1)
在继续深入学习之前,现在有必要敲敲代码。将上文的思路实现出来。
树的构造
struct node {
int L, R, V;
} nd[N * 4];
建树
void build(int p, int L, int R) {
nd[p] = {
L, R, 0};
if (L == R)
return;
int mid = L + R >> 1;
build(p << 1, L, mid);
build(p << 1 | 1, mid + 1, R);
}
注意,在我们建树的时候,我们将mid分配给了左子树。
并且,当L==R,即长度为1的时候,我们就return,当长度为2的时候,再进行mid,从中间砍掉,分为左子树和右子树。
修改
void modify(int p, int L, int R, int v) {
if (nd[p].L >= L && nd[p].R <= R) {
nd[p].V += V; //对本节点的V值进行累加,就相当于历史记录一样。
return;
}
int mid = nd[p].L + nd[p].R >> 1;
if (L <= mid) {
//进入左子树
modify(p << 1, L, R, v);
}
if (R > mid) {
modify(p << 1 | 1, L, R, v);
}
}
查询(单点查询)
void query(int p, int x) {
//计算x节点上的v值
total += nd[p].V;
if (nd[p].L == nd[p].R)
return;
int mid = nd[p].L + nd[p].R >> 1;
if (x <= mid) {
query(p << 1, x);
} else {
query(p << 1 | 1, x);
}
}
total是一个全局的变量,负责+=查询到最后节点这一路径上的V累加值。
最后a[x-1]+total即答案,total就是一个History历史记录。
和我们上文所说的思想是一致的。
延迟标记
树的结构
现在,为了更高效地支持区间查询,我们不得不使得线段数节点修改一下。
我们修改完毕的线段数节点结构如下:
struct node {
int L, R, sum;
} nd[N * 4];
没错,现在,我们将V修改为sum,意义也开始变得不同,现在,这个节点的sum代表着的是L到R范围的所有元素之和,为sum。
例如:a = [1, 2, 3, 4]
那么现在树的结构如下,例如对(1)号节点,它的范围是1-4所以 s u m = 10 sum=10 sum=10。

其中,我们有一种关系:即nd[i].sum=nd[i<<1].sum+nd[i<<1|1].sum父节点的sum为子节点sum之和。
这样树的结构,方便我们进行区间查询例如,现在sum就是在进行区间查询这一段总和是多少。
区间查询
我们要查询1-3范围综合是多少,那么就是(2)号节点的sum和(6)号节点的sum。和前文查询的思路是一模一样的,(2)号节点记录了1-2范围的sum是多少,而(6)号节点记录了3-3范围的sum是多少,最后答案是,6。
区间查询结束了。算法大体的思路是这样,代码在后文给出。
区间修改
对于本次的区间修改,例如,我们想修改区间1-3,然后加2。
那么对于(1)号节点来说,它是 10 + 3 ∗ 2 10+3*2 10+3∗2 其中,3指的是1-3区间长度,每个元素加2,所以加了6。
让我们来直接看图。
完成上图的代码如下:
(摘自博客:https://blog.csdn.net/weixin_45697774/article/details/104274713)
void add(int i,int l,int r,int k)
{
if(tree[i].r<=r && tree[i].l>=l)//如果当前区间被完全覆盖在目标区间里,讲这个区间的sum+k*(tree[i].r-tree[i].l+1)
{
tree[i].sum+=k*(tree[i].r-tree[i].l+1);
tree[i].lz+=k;//记录lazytage
return ;
}
push_down(i);//向下传递
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
return ;
}
首先请无视poshdown(i)。对于上图,我们会发现,这其中存在着几个错误的节点,例如,节点(4)和节点(5)。他们的sum值并没有被修改成功。这是因为,在add函数之中,当tree[i].r<=r && tree[i].l>=l我们就return了。一种方法是,我们直接把return去掉,当然,其实我们还有另一种方法,引入延迟标记。
修正错误,以及何时修正错误
当我们访问到(4)号和(5)节点的时候,我们再进行修复错误。
对,延迟就是差不多这个意思,我们延迟到:当我们会访问到这个节点的时候,我们再修复这个节点的错误。
延迟标记怎么设置呢,改进Node的Struct,新增一个lz变量。
struct node {
int L, R, sum, lz;
} nd[N * 4];
对于访问到某个节点来说,它拥有一个lz,就说明,它需要更新。
对于pushdown来说,它的意义是:
(1)清空本节点的lz标记
(2)更正左右子节点的sum(以本节点的lz标记为准)。
(3)将本节点的lz加入到左右子节点的lz标记上去。(这样可以实现层层传递这个lz标记,访问到哪里,标记传递到哪里)
请看pushdown的代码:
(摘自博客:https://blog.csdn.net/weixin_45697774/article/details/104274713)
void push_down(int i)
{
if(tree[i].lz!=0)
{
tree[i*2].lz+=tree[i].lz;//左右儿子分别加上父亲的lz
tree[i*2+1].lz+=tree[i].lz;
int mid=(tree[i].l+tree[i].r)/2;
tree[i*2].sum+=tree[i].lz*(mid-tree[i*2].l+1);//左右分别求和加起来
tree[i*2+1].sum+=tree[i].lz*(tree[i*2+1].r-mid);
tree[i].lz=0;//父亲lz归零
}
return ;
}
查询的代码:
inline int search(int i,int l,int r){
if(tree[i].l>=l && tree[i].r<=r)
return tree[i].sum;
if(tree[i].r<l || tree[i].l>r) return 0;
push_down(i);
int s=0;
if(tree[i*2].r>=l) s+=search(i*2,l,r);
if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);
return s;
}
需要注意的是,pushdown的时机,那就是,当访问本节点旗下的左右子节点的时候。
请见谅,由于篇幅限制,您可以访问:https://blog.csdn.net/weixin_45697774/article/details/104274713 大佬的博客,查看完整的代码。
乘法线段树
它的意思是,相较于之前求区间和,只有Add操作的线段树,我们现在引入了Mul乘法。
例如,对区间[1,2]每个元素乘2
简单来说,它的数据结构其实没有什么变化,比如节点中有sum变量。延迟标记稍有不同,它分为2个延迟标记,一个是plz,一个是mlz。前者是加法的延迟标记,后者是乘法的延迟标记。
我们认为,本节点的总和是sum,那么通过延迟标记修改完毕的sum是 s u m = s u m ∗ m l z + p l z sum=sum*mlz+plz sum=sum∗mlz+plz
所以维护两个延迟标记就显得非常重要。
我们维护加法的时候,比如Add函数,那么打上plz标记就是一句话的事情plz+=v
那么维护乘法的时候,比如Mul函数,那么这个时候需要同时修改plz和mlz,它们都需要*=v
这就好像我们原来有一个 ( m l z ∗ m + p l z ) ∗ v (mlz*m+plz)*v (mlz∗m+plz)∗v一样。展开括号即可知道为什么需要同时修改plz和mlz。
现在给出,pushdown的代码:
(摘自博客:https://blog.csdn.net/weixin_45697774/article/details/104274713)
inline void pushdown(long long i){
//注意这种级别的数据一定要开long long
long long k1=tree[i].mlz,k2=tree[i].plz;
tree[i<<1].sum=(tree[i<<1].sum*k1+k2*(tree[i<<1].r-tree[i<<1].l+1))%p;//
tree[i<<1|1].sum=(tree[i<<1|1].sum*k1+k2*(tree[i<<1|1].r-tree[i<<1|1].l+1))%p;
tree[i<<1].mlz=(tree[i<<1].mlz*k1)%p;
tree[i<<1|1].mlz=(tree[i<<1|1].mlz*k1)%p;
tree[i<<1].plz=(tree[i<<1].plz*k1+k2)%p;
tree[i<<1|1].plz=(tree[i<<1|1].plz*k1+k2)%p;
tree[i].plz=0;
tree[i].mlz=1;
return ;
}
主席树
主席树其实很简单 ,它没有什么特别的地方。它也是一种线段树。
它常常用来区间查询第K大的问题。
树的结构
我们想象有这么这么一颗树,它的L,R不再代表着的是区间。而是值域。而这个节点的sum代表着的是,这个值域中,有多少数字。
我们来举个栗子,对于数组a = [1, 3, 4]
它的值域是[1,4]所以根据值域进行Dfs建树。
这里要注意的是,因为是按照Dfs建树,和之前的节点编号顺序稍有不同。
建造出这颗树有什么用呢,有了这棵树,我们就可以轻松的来查询第K大到底在哪里。
方法:缩小值域范围。
先给出建树的代码:
int build(int l, int r) {
//您可以按照这个建树逻辑学习一下
int rt = ++tot; //本节点的编号
sum[rt] = 0;
if (l < r) {
int mid = (l + r) >> 1;
lson[rt] = build(l, mid);
rson[rt] = build(mid + 1, r);
}
return rt;
}
tot是总共树的节点编号。我们建树的时候采用动态开点,然后lson数组记录节点的左子树的节点编号,rson数组记录本节点的右子树编号。然后现在sum为0,sum记录了当前这个值域我们有多少数。我们以后再加入进去。return rt返回当前节点的编号。那么对于最外层的build函数,它返回的也就是树根编号。这将在下文我们进行讨论。
查询第K大
还是上面的这个线段数的图,我们知道(1)号节点,在值域[1,4]中我们有3个数字。所以查找第2大数字的时候,我们首先知道第二大的这个数字应该在[1,4]这个区间内。
然后对于(2)号节点,我们知道[1,2]区间内有1个数字,所以第2大数字,不应该在区间[1,2]内,因为这个区间只包含一个数字,所以应该在(5)号节点[3,4]区间内。而因为[1,2]内已经有1个数字了,所以查询第2大,就是查询在[3,4]内的第1大数字。进入(5)号节点,开始查询第一大数字,发现(5)号节点的左子树(6)在区间[3,3]有一个数字,所以进入,因为我们现在查询的是第一大数字。
现在值域被缩小为[3,3],所以在a数组[1, 3, 4]中,第二大数字就是3。
根据这颗值域线段树,我们就能查询出第K大问题。
root数组
我们刚刚上面查询的是第K大数字,它查询的区间的全域,也就是在所有范围内的第K大。
还是对于a = [1, 3, 4]在a的区间[2,3]查询第二大数字(答案是4,a区间从1开始),那么这个时候该怎么办呢?
我们使用一个root数组,来保存树根,历史记录。
什么意思呢,也就是,刚刚我们建树的时候,sum是0嘛,那么我们插入a[i]的时候,我们会新建一颗树。然后把这颗新建的树的树根保存在root数组。
比如,对于a数组,我们在值域线段数加入完a[1]之后,我们就把这颗线段树保存在root[1]之中,当我们加入a[2]到这颗线段树,注意这颗线段树现在包含a[1],a[2],我们就把树根保存在root[2]之中,当我们加入a[3]的时候,就把这颗线段树的树根保存在root[3]之中。
代码将在稍后给出。
我们来看看root[1]和root[3]:
现在,我们查询a的区间[2,3]那么在这个区间,root[3]中处于值域[1,4]有3个数,而处理完第一个节点也就是a[1]的时候,root[1]中,处于值域[1,4]的有1个数,所以我们可以推测出,a[2],a[3]位于[1,4]的,有2个数。
算法就是 s u m [ r o o t [ 3 ] ] − s u m [ r o o t [ 1 ] ] sum[root[3]]-sum[root[1]] sum[root[3]]−sum[root[1]]。
也就是{a[1]、a[2]、a[3]}-{a[1]}
那么对于值域[1,2]我们有几个数字呢?现在的情况还是用sum[root[3]->lson]-sum[root[1]->lson]得到0,所以在a的区间[2,3]查询第2大,只能在区间[3,4]里面找,剩下的都一样。
这里只是想向您说明,我们到底是怎么知道在值域之中,我们有多少个数字的。那就是通过root数组查询历史记录,更正线段数节点值域范围即可。然后再把值域区间缩小到L==R。即可找到这个数字是几。
动态开点建树
这里和root数组是结合在一起的,其实这篇博客写的比较口语化,它的真正性质叫做“可持久化”。
在main函数之中,我们有:
main()
for (int i = 1; i <= n; i++) {
a[i] = lower_bound(b + 1, b + nn + 1, a[i]) - b;
root[i] = update(root[i - 1], 1, nn, a[i]);
}
请先忽视a[i] = lower_bound(b + 1, b + nn + 1, a[i]) - b;这句话将在后文离散化介绍。
update()
int update(int p, int l, int r, int x) {
int rt = ++tot;
lson[rt] = lson[p], rson[rt] = rson[p], sum[rt] = sum[p] + 1;
if (l < r) {
int mid = (l + r) >> 1;
if (x <= mid)
lson[rt] = update(lson[rt], l, mid, x);
else
rson[rt] = update(rson[rt], mid + 1, r, x);
}
return rt;
}
我个人觉得这个博主讲解的特别好,下文图片粘贴自:https://blog.csdn.net/Foxreign/article/details/118770162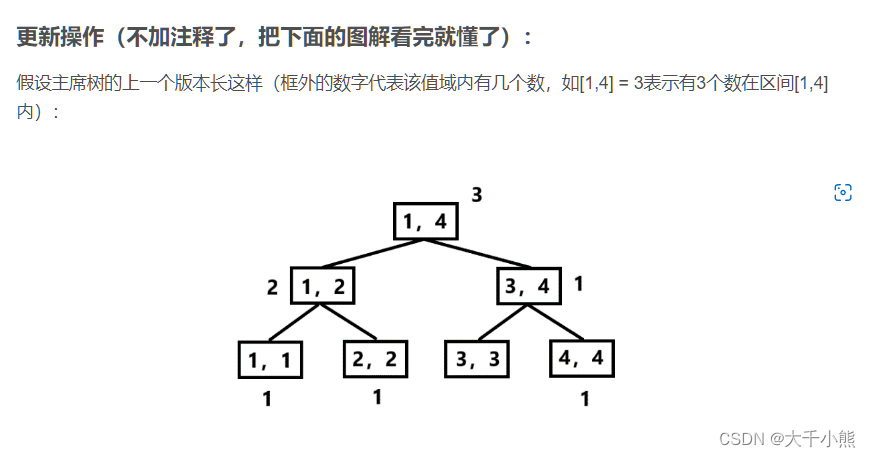

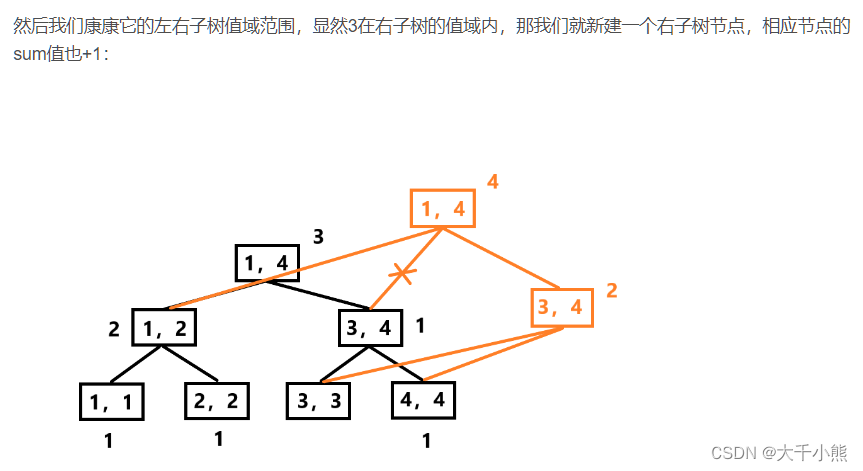
然后再进行递归操作,进入左子树或者右子树。
请去大佬博客学习。
简单来说,就是每次Update,都会新开一个根节点,我们把这个根节点保存在了root数组之中。
离散化
下面就是离散化了,我们为什么需要离散化。
比如这是我们原来的a数组:a = [10, 7, 9, 3]
那我们建树难道值域就要建树成[3,10]嘛?
这,有点开销太大了,因为最后子节点可能会是:[3,3]、[4,4]、[5,5]…[10,10]
有很多节点是用不到的,浪费了。
所以我们可以做一个这样的离散化,那就是a[i]存储的是,我在整个序列中,我是第几大的数字
比如现在离散化完毕之后:a = [4 2 3 1]
a[1]=10,它是整个序列中第四大数字,所以它是4。
这样的话,a数组离散化之后,它的值域就变成了[1,4]
值域末尾确定,就是我们离散化了几个数字。请看代码来理解。
现在,如果我们查询一个区间的结果是,值域[3,3],我们应该直接输出3嘛?不是,这个3是离散化后的结果,它的意思是第三大的数,所以真正对应非离散化的结果它是9,输出9才对。
好,让我们来看下代码:
n = read(), m = read(), tot = 0;
//离散化
for (int i = 1; i <= n; i++)
a[i] = b[i] = read();
sort(b + 1, b + n + 1); // b是离散化的结果
int nn = unique(b + 1, b + n + 1) - b - 1;
root[0] = build(1, nn);
for (int i = 1; i <= n; i++) {
a[i] = lower_bound(b + 1, b + nn + 1, a[i]) - b;
root[i] = update(root[i - 1], 1, nn, a[i]);
}
读入完成之后,先把a数组的数据保存到b里面,然后对b进行unique函数,最后对查找a[i]在b中是第几大,写回a[i]中,完成离散化。并且将离散化的值,插入到值域线段树中。
这就是一颗,主席树。
下面请看例题,再次想想。
例题
描述:
Give you a sequence and ask you the kth big number of a inteval.
输入:
The first line is the number of the test cases.
For each test case, the first line contain two integer n and m (n, m <= 100000), indicates the number of integers in the sequence and the number of the quaere.
The second line contains n integers, describe the sequence.
Each of following m lines contains three integers s, t, k.
[s, t] indicates the interval and k indicates the kth big number in interval [s, t]
输出:
For each test case, output m lines. Each line contains the kth big number.
不知道A不AC的代码:
//修改自博主:https://blog.csdn.net/Foxreign/article/details/118770162
#include <algorithm>
#include <iostream>
#define rep(i, x, y) for (int i = (x); i <= (y); i++)
#define down(i, x, y) for (int i = (x); i >= (y); i--)
#define MAXN 1001
using namespace std;
int a[MAXN], b[MAXN], root[MAXN], lson[MAXN << 5], rson[MAXN << 5], sum[MAXN << 5];
int st, ed, k;
int n, m, tot = 0;
inline int read() {
int x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
int build(int l, int r) {
int rt = ++tot;
sum[rt] = 0;
if (l < r) {
int mid = (l + r) >> 1;
lson[rt] = build(l, mid);
rson[rt] = build(mid + 1, r);
}
return rt;
}
int update(int p, int l, int r, int x) {
int rt = ++tot;
lson[rt] = lson[p], rson[rt] = rson[p], sum[rt] = sum[p] + 1;
if (l < r) {
int mid = (l + r) >> 1;
if (x <= mid)
lson[rt] = update(lson[rt], l, mid, x);
else
rson[rt] = update(rson[rt], mid + 1, r, x);
}
return rt;
}
int query(int u, int v, int l, int r, int k) {
if (l == r)
return l;
int x = sum[lson[v]] - sum[lson[u]];
int mid = (l + r) >> 1;
if (x >= k)
return query(lson[u], lson[v], l, mid, k);
else
return query(rson[u], rson[v], mid + 1, r, k - x);
}
int main(int argc, char const* argv[]) {
int t = read();
while (t--) {
n = read(), m = read(), tot = 0;
//离散化
for (int i = 1; i <= n; i++)
a[i] = b[i] = read();
sort(b + 1, b + n + 1); // b是离散化的结果
int nn = unique(b + 1, b + n + 1) - b - 1;
root[0] = build(1, nn);
for (int i = 1; i <= n; i++) {
a[i] = lower_bound(b + 1, b + nn + 1, a[i]) - b;
root[i] = update(root[i - 1], 1, nn, a[i]);
}
rep(i, 1, m) {
st = read(), ed = read(), k = read();
printf("%d\n", b[query(root[st - 1], root[ed], 1, nn, k)]);
}
}
return 0;
}
参考文档与补充说明:
本博客大量参考了下列博客,再次表达由衷地感谢。
线段数详细讲解以及模板例题:https://blog.csdn.net/weixin_45697774/article/details/104274713(包含了除法|根号线段树)
主席树清晰讲解:https://blog.csdn.net/Foxreign/article/details/118770162
大量习题:
(下面包含了一道扫描线的例题)
https://blog.csdn.net/weixin_42638946/article/details/115512941
边栏推荐
- 23. Network principle - key protocols in tcp/ip four layer model (2)
- 【sklearn报错解决方案】UndefinedMetricWarning: Precision is ill-defined and being set to 0.0
- How to apply neural network model to practice - mathematical modeling case of neural network model
- Opencv (12): cv:: rectangle learning and code demonstration, using OpenCV to draw rectangles / rectangular boxes
- Shuttle + alluxio accelerated memory shuffle take-off
- Data analysis children's shoes can't be missed | operational risk control business analysis report
- LED light of 51 single chip microcomputer
- powershell和cmd区别
- Vs2017 opencv3.4.2 is compiled into x86 through the release version source code
- JUC_synchronized关键字详解
猜你喜欢

Why learn istio
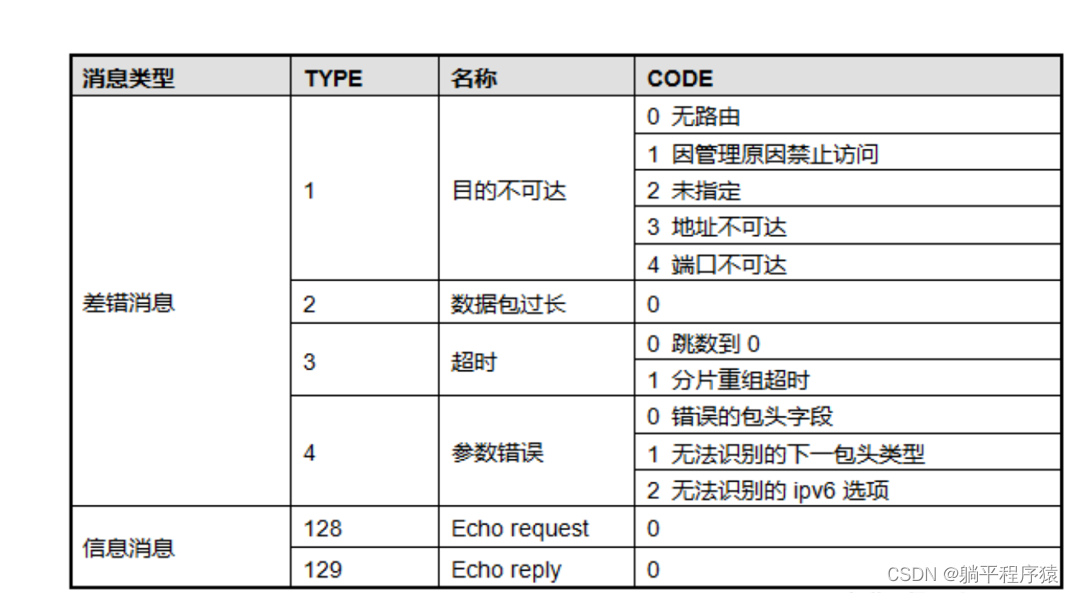
Ipv6-icmpv6 protocol
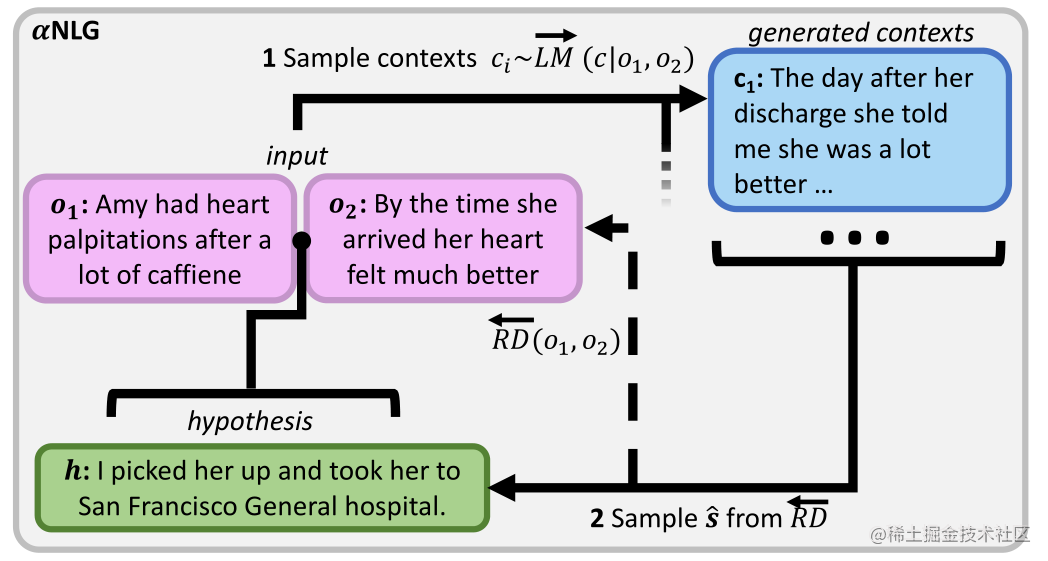
Reflective Decoding: Beyond Unidirectional Generation with Off-the-Shelf Languag

Chinese synonymous sentence online converter - Chinese synonymous sentence converter software

Starbucks may close more U.S. stores in the future due to concerns about the safety of employees

Understand the MySQL architecture design in one article, and don't worry about the interviewer asking too much

出于对员工人身安全的担忧 星巴克未来可能关闭更多美国门店

【深度学习】pytorch使用tensorboard可视化实验数据

CDH之impala

Synoxos TCP data segment sending process
随机推荐
Phpcms add multi text attribute field_ Detailed tutorial
Digital image processing (Gonzalez) learning Chapter II fundamentals of digital image
信奥中的数学学习:小学、初高中数学 视频集
[wechat applet] breakpoint debugging I
Virtual exhibition combines AI digital people to help enterprises solve the current dilemma
Attribute operation of DOM series elements
Understand 25 neural network models - typical models of artificial neural networks
Keep the number of float type to 2 decimal places
【通信】【2】《宽带太赫兹通信技术》的笔记和一些简单的词汇的意思(误
argparse库的基本使用
Pyqt5 learning resource preparation and environment configuration
LeetCode_93_复原IP地址
Read the paper: (yolov1) you only look once:unified, real time object detection
Gauss mathematics -- watching animation and Learning Mathematical Olympiad
Win7 installation system, no tricks
Synoxos TCP data segment sending process
UE GIS虚拟化的学习
kvm部署及应用
Essential certificate for product manager!
Goto of C language