当前位置:网站首页>Force deduction record: dynamic programming 2 knapsack problem (1) 01 knapsack - 416 split equal sum subset, 1049 weight of the last stone II, 494 target sum, 474 one and zero
Force deduction record: dynamic programming 2 knapsack problem (1) 01 knapsack - 416 split equal sum subset, 1049 weight of the last stone II, 494 target sum, 474 one and zero
2022-07-21 22:47:00 【Kiwi_ fruit】
This topic
- 416 To divide into equal and subsets
- 1049 The weight of the last stone II
- 494 Objectives and
- 474 One and zero
01 knapsack
- 01 knapsack : Capacity of w The backpack ,n Items , The first i The weight of the item is weight[i], Value is value[i], Each item can only be loaded once , Which items are expected to have the greatest total value .
- A two-dimensional dp Array 01 knapsack :
- Definition dp[i][j] Indicates from subscript [0-i] Take whatever you want from your belongings , Put in capacity j The backpack , What is the maximum total value ;
- Recursion formula can also be used as a backpack i When it comes to items ,dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
- initialization dp[i][0] = 0, When the backpack capacity j Less than 0 The weight of each item weight[0] when ,dp[0][j] = 0, otherwise dp[0][j] = value[0];
- Traversal order from small to large , Here, first traverse the items and then the backpack ;
- give an example .
- One dimensional scrolling array 01 knapsack :
- Define a one-dimensional array d[j] Indicates the upper layer (i - 1) Copy to current layer (i), Instant items i The filling capacity is j The maximum total value of your backpack ;
- The recursive formula dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
- Items grow from small to large , Backpack from big to small ( Because the upper layer covers the current layer , Prevent the same item from being placed multiple times );
- The traversal order can only be items first and then backpacks ;
- give an example . It is recommended to use a one-dimensional rolling array .
416 To divide into equal and subsets
- 01 knapsack DP:
- Definition dp[j] The capacity is j The backpack , The maximum sum of the numbers put in is dp[j], The length is the target and plus 1;
- The recursive formula dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
- Initialize to full 0( Less than the value of goods );
- Traversal order traverses the items first ( From small to large ) And then traverse the backpack ( From big to small );
- give an example .
class Solution {
public boolean canPartition(int[] nums) {
int leng = nums.length;
// Judge special cases
if(leng == 1) return false;
// Find the target value
int sum = 0;
for(int i = 0; i < leng; i++){
sum += nums[i];
}
// Not even return false
if(sum % 2 == 1) return false;
int target = sum / 2;
// Definition dp[j] The capacity is j The backpack , The maximum sum of the numbers put in is dp[j]
// The length is the target and plus 1
// Initialize all 0
int[] dp = new int[target + 1];
// Traversal order traverses the items first ( From small to large ) And then traverse the backpack ( From big to small )
for(int i = 0; i < leng; i++){
for(int j = target; j >= nums[i]; j--){
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
// Return results
return dp[target] == target;
}
}
1049 The weight of the last stone II
- ditto 416 To divide into equal and subsets , Exchange items for stones , Or divide the stones into two piles with the same weight .
- Definition dp[j] The capacity is j The maximum weight of your backpack is dp[j] The stone of ;
- The recursive formula dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
- take dp[0] Initialize to 0, The length is half of the maximum weight ;
- Traversal order traverses the items first ( From small to large ) And then traverse the backpack ( From big to small );
- give an example .
- Be careful : Round down when taking the target weight , therefore dp The weight of the array is smaller .
class Solution {
public int lastStoneWeightII(int[] stones) {
// Judge special cases
int leng = stones.length;
if(leng == 1) return stones[0];
int sum = 0;
for(int i = 0; i < leng; i++){
sum += stones[i];
}
int target = sum / 2;
// Definition dp[j] The capacity is j The maximum weight of your backpack is dp[j] The stone of
// take dp[0] Initialize to 0, The length is half of the maximum weight
int[] dp = new int[target + 1];
// Traversal order traverses the items first ( From small to large ) And then traverse the backpack ( From big to small )
for(int i = 0; i < leng; i++){
for(int j = target; j >= stones[i]; j--){
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
// Return results
return sum - 2 * dp[target];
}
}
494 Objectives and
- 01 knapsack DP( Combine ):
- Definition dp The array represents a capacity of j The back package of the addition is filled with dp[j] Methods ;
- The recursive formula dp[j] += dp[j - nums[i]];
- initialization dp[0] = 1, The length is the sum of the target value plus the array divided by 2( Add 1);
- Traversal order first item ( From small to large ) And backpacking ( From big to small );
- give an example .
- Be careful : When the sum of the target number and the array cannot be 2 Division without result .
class Solution {
public int findTargetSumWays(int[] nums, int target) {
// Definition dp The array represents a capacity of j The back package of the addition is filled with dp[j] Methods
int sum = 0;
for(int i = 0; i < nums.length; i++) sum += nums[i];
// When the sum of the target number and the array cannot be 2 Division without result .
if((sum + target) % 2 != 0) return 0;
int t = (sum + target) / 2;
// Target less than 0 The time is reversed
if(t < 0) t = -t;
int[] dp = new int[t + 1];
// initialization dp[0] = 1
dp[0] = 1;
// Traversal order first item ( From small to large ) And backpacking ( From big to small )
for(int i = 0; i < nums.length; i++){
for(int j = t; j >= nums[i]; j--){
dp[j] += dp[j - nums[i]];
}
}
// Return results
return dp[t];
}
}
474 One and zero
- 01 knapsack DP:
- Definition dp[i][j] Express : At most i individual 0 and j individual 1 Of strs The size of the largest subset of is dp[i][j];
- The recursive formula :dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
- initialization dp[0] = 0;
- Traversal order first item ( From small to large ) And backpacking ( A two-dimensional , From big to small );
- give an example .
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
// Definition dp[i][j] Express : At most i individual 0 and j individual 1 Of strs The size of the largest subset of is dp[i][j]
int[][] dp = new int[m + 1][n + 1];
// Statistics of string types 0 and 1 Number
for(String str : strs){
int zeroNum = 0;
int oneNum = 0;
char[] s_arr = str.toCharArray();
for(char s : s_arr){
if(s == '1'){
oneNum += 1;
}else{
zeroNum += 1;
}
}
// Traversal order first item ( From small to large ) And backpacking ( A two-dimensional , From big to small )
for(int i = m; i >= zeroNum; i--){
for(int j = n; j >= oneNum; j--){
dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
// Return results
return dp[m][n];
}
}
边栏推荐
猜你喜欢

International Bluetooth giant Nordic enters the WiFi field

This Bluetooth chip giant aims at the WiFi SOC market and launches a low-power WiFi MCU product line

Expression evaluation

Cocos creator 3.2 realizes the complete effect of 2D map 3D character 45 degree RPG game

Why is Le Xin in a hurry to release esp32-c3 when there are few words

004: print characters
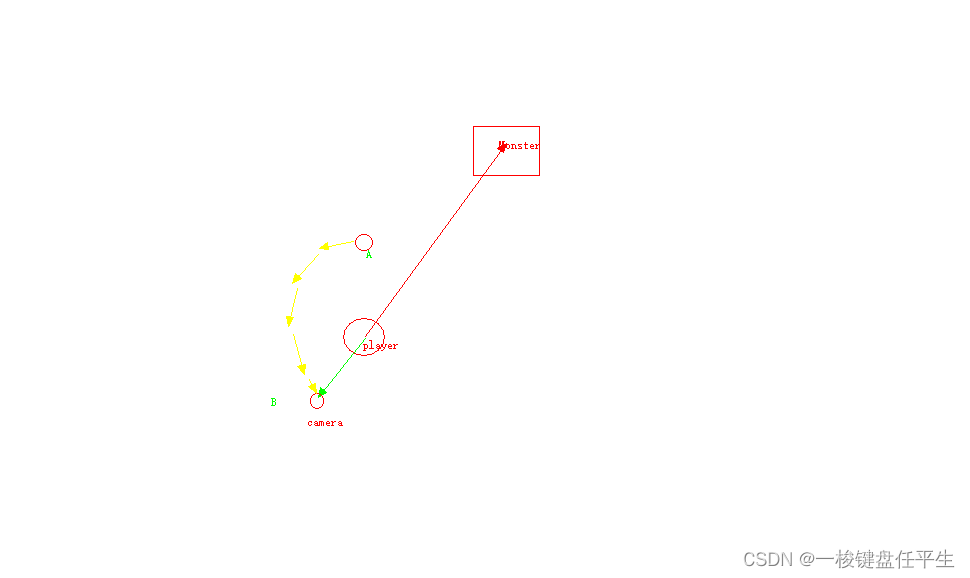
unity 锁定相机绕锁定目标的弧形运动

567. Arrangement of strings
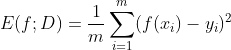
Watermelon book chapter 2 Notes - Performance Measurement

Property analysis of matter protocol (II) multiple fabric and permission control
随机推荐
卡牌
一个好用的Unity Touch管理器
Expression evaluation
543. Diameter of binary tree
力扣记录:动态规划5子序列问题(1)——300 最长上升子序列,1143 最长公共子序列,1035 不相交的线,674 最长连续递增序列,718 最长重复子数组,53 最大子序和
226. Flip binary tree
HoloLens下载、读取与存储Json文件路径问题(个人Hololens2进阶开发小总结一)
力扣记录:动态规划3打家劫舍——198 打家劫舍,213 打家劫舍II,337 打家劫舍III
[oops framework] supporting hot update plug-ins
Upgrade every day
Verify Goldbach conjecture
108. Convert an ordered array into a binary search tree
Probability theory - maximum likelihood estimation
XML详解
n factorial
Small practice: implementing myArray
Probability theory - variance and covariance, correlation coefficient
2022acm summer training weekly report (I)
567. Arrangement of strings
International Bluetooth giant Nordic enters the WiFi field