hidden Markov model (HMM)Hidden Markov Model

· Definition

Hidden Markov model is a probability model of time series • Describe the random generation of unobservable state sequences by a hidden Markov chain (state sequence), Then generate a Observation results in observation sequence (observation sequence) The process of , Each position of the sequence can be regarded as a moment .

for instance ：
Weather and ice cream
Imagine you are 2799 Climatologist in , Studying the history of global warming , You can't find any Beijing 2020 The weather records of the summer , But you found Xiao Ming's diary , It lists the number of ice cream Xiao Ming eats every day this summer .
Our goal is ： According to the observation （ The number of ice cream Xiao Ming eats every day in summer ） Estimate the weather every day in summer
Suppose the weather is only cold (COLD) And heat (HOT) Two possible , Xiao Ming eats only 1、2、3 Three possibilities , So your task is ：
1. Given the observation sequence O , such as O = {3,1,3} （ Each integer represents the number of ice cream Xiao Ming ate that day ）
2. Find out the hidden sequence of weather states Q, such as Q= (HOT,COLD,HOT)

among ：
Q={q1,q2,…,qN} A collection of all possible states (N individual )
V={v1,v2,…,vN} A collection of all possible observations (M individual )
I={i1,i2,…,iN} The length is T The state sequence of , Each comes from Q
O={o1,o2,…,oN} The length is T The sequence of observations , Each comes from V
π=(πi) Initial state probability vector
A=[aij]NN State transition probability matrix
B=[bj(ot)]NM Observation probability matrix

An expression

therefore HMM The expression of is ： λ=(π,A,B)

Two hypotheses

1. Homogeneous Markov hypothesis ： Hidden Markov chains at the moment t The state of is only related to t− 1 The state of

2. Observation independence Hypothesis ： The observation is only related to the state at the current moment

Three basic questions

1.evaluation（ The problem of probability calculation ）
• Known models λ=(π,A,B) And the observation sequence O=(o1,o2,…,oT)
• Calculate the probability P(O|λ)
Solution ： Forward algorithm , Backward algorithm

2.learning( Learning problems )
• Known observation sequence O=(o1,o2,…,oT)
• Estimation model λ, send P(O|λ) Maximum
Solution ：Baum-Welch Algorithm （ That is to say EM The predecessor of the algorithm ）

3.decoding( Decoding problem )
• Known models λ=(π,A,B) And the observation sequence O=(o1,o2,…,oT)
• Calculation makes probability P(I|O) The largest sequence of States I=(i1,i2,…,iT)
Solution ：Viterbi Algorithm

· Forward algorithm （ Ask for results ）

Forward probability definition

Given a hidden Markov model λ , Define to time t Part of the observation sequence is o1,o2,…,oG And the state is qi Of Probability is forward probability , Write it down as （ Omission λ ）:

• The key of forward algorithm ：

The reason for reducing the amount of calculation is that every calculation , Directly quote the calculation result of the previous time , Avoid double counting .
Complexity goes from O(TN^T) drop to O(TN^2)
prove ：

1. Bayes' formula

2. Edge distribution

3.HMM Two basic assumptions of 、 Bayes' formula 、 Edge distribution

· Backward algorithm （ Pursuing cause ）

Backward probability definition

Given a hidden Markov model λ, Define at the moment t Status as qi Under the condition of , from t+ 1 To T Partial view of The test sequence is o(t+1),o(t+2),…,O(T) The probability of is backward , Write it down as （ Omission λ ）:

prove ：

·Baum-Welch Algorithm

Baum-Welch The algorithm can solve the hidden Markov problem of unsupervised learning , That is said , If we now have a training set without a state sequence , Only the observation sequence , Now let's find the parameters of hidden Markov model and ：λ=(π,A,B). So you can use it Baum-Welch Algorithm to solve the problem .

① $p(O|{\lambda }^t)$ and $\lambda$ irrelevant , Therefore, it can be directly removed , there t Should be (t), Not power

② Observation independence hypothesis restraint , The red line is irrelevant , Go to

·Viterbi Algorithm

• Using dynamic programming to find the path with maximum probability （ The best path ）, A path corresponds to a sequence of States
• The characteristics of the optimal path ： If the optimal path is at time t Pass node i(t)* , Then this path starts from the node i(t)* In the end spot i(T)* Part of the path , From i(t)* To i(T)* For all possible partial paths , Must be optimal
• Just from the moment t = 1 Start , Recursively calculate at the moment t Status as i The maximum probability of each partial path , Until you get the moment t= T Status as i The maximum probability of each path , moment t = T The maximum probability of is the most Probability of optimal path P* , The end point of the optimal path i(T)* Also get
• after , In order to find the nodes of the optimal path , From the endpoint i(T)* Start , From the back to the front, get the node step by step i(T)* , … , i(1), Get the best path I = (i(1),i(2),…,i(T)* )

· Example

Use two examples to explain

Eg1.

Draw the ball as follows , An observation sequence that produces the color of the ball ：
• Start ： Equal probability random selection 4 One of the boxes , Draw a ball randomly from the box , Record colors , Put back ;
• then , Randomly move from the current box to the next box , Draw a ball randomly from the next box , Record colors , Put back ;
• Transfer rules ：
• The box 1 → It must be a box 2
• The box 2 or 3 → P = 0.4 On the left ,P = 0.6 On the right
• The box 4 → P = 0.5 The box 4,P = 0.5 The box 3
• The observer can only observe the sequence of colors of the ball , We can't see which box the ball came from
• Observation sequence （ Observable ）： Sequence of ball colors ; Sequence of States （ Hidden ）： Sequence of boxes
• repeat 5 Time ： Observation sequence O= { red , red , white , white , red }

1. An expression , find λ=(π,A,B)

among ：
State set ：Q ={ The box 1, The box 2, The box 3, The box 4} , N = 4
Observation set ：V ={ red , white } , M = 2
Initial probability distribution ：π= {0.25, 0.25, 0.25, 0.25 }T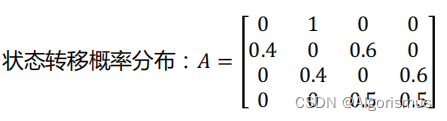


End answer ~

Eg2.

Consider the box and ball model λ=(π,A,B) , State set Q = {1,2,3} , Observation set V={ red , white }

set up T = 3,O = { red , white , red } , put questions to ：
· Calculate with forward algorithm and backward algorithm P(O|λ)
· Find the optimal path I*=(i(1),i(2),i(3)*)

2. Forward algorithm ：

3. Backward algorithm

4.Viterbi Algorithm

The best path of the conditional ball of the second question I*=(i(1),i(2),i(3)*)
Explain ： As shown in the figure below , Choose the best path among all possible paths , Follow the steps below

Actual operations Address
Reference material ：
【 machine learning 】【 Whiteboard derivation series 】【 Collection 1～33】_ Bili, Bili _bilibili
Baum-Welch Algorithm - happy _00 - Blog Garden
HMM—— Backward algorithm of probability calculation problem （ 5、 ... and ） - You know

Thank you for watching. ~