Signal noise reduction method

The Fourier transform

Only the frequency components of a signal can be obtained , But we don't know when the ingredients appear .“ For nonstationary processes , Fourier transform has limitations ”.

The short-time Fourier transform （Short-time Fourier Transform, STFT）

The whole time-domain process is decomposed into countless small processes of equal length , Each small process is approximately stationary , Fourier transform again , You know what frequency appears at which time point . But the width of window function is hard to define . Narrow window time resolution is high 、 Low frequency resolution , Wide window time resolution is low 、 High frequency resolution . For time-varying unsteady signals , High frequency is suitable for small windows , Low frequency is suitable for large windows . However STFT The windows of are fixed , In a STFT The width does not change in , therefore STFT Still unable to meet the frequency requirements of unsteady signal changes .

Wavelet transform

Wavelet transforms the basis of Fourier transform —— The infinitely long trigonometric function basis is replaced by the infinitely long attenuated wavelet basis . Can get frequency and Time frequency .

The basis function will scale 、 Will pan （ In fact, the essence is not translation , But the decomposition of two orthogonal bases ）. Narrow , Corresponding to high frequency ; Stretch wide , Corresponding to low frequency . Then the basis function is multiplied by the signal . A certain scale （ Width ） The result of lower multiplication , It can be understood as the number of frequency components corresponding to the current scale contained in the signal . therefore , The basis function will be at some scale , Multiply with the signal to get a large value , Because there is a coincidence between the two . Then we can know how many components of the frequency the signal contains .

wavelet The difference in Fourier transform lies in , The infinitely long trigonometric function basis is replaced by the infinitely long attenuated wavelet basis . Wavelet transform has two variables ： scale a（scale） Peaceful migration τ（translation）. scale a Control the scaling of wavelet function , Translation τ Control the translation of wavelet function . The scale corresponds to the frequency （ inverse ratio ）, Translation τ It corresponds to time .
For abrupt signals , Gibbs effect exists in Fourier transform , We can't fit the mutation signal well with infinite trigonometric function .

Wavelet decomposition , The energy of the signal is mainly distributed on the scale function of low resolution , The energy distribution of noise remains unchanged , It is still evenly distributed on all wavelet coefficients . therefore , Wavelet threshold denoising method is to retain or shrink large wavelet coefficients ( Low frequency coefficient ), Eliminate small wavelet coefficients ( High frequency coefficient ). When using wavelet threshold method to denoise spectral data , Choosing different threshold functions reflects different processing strategies for wavelet sparse modulus , Usually, the threshold function is used Donoho Waiting for the article “Ideal Spatial Adaptat1n by Wavelet Shrinkage”(B1metrika, Vol.81, N0.3,pp.425-455,1994) Proposed hard threshold function (Hard Threshold Funct1n) And soft threshold function (Soft Threshold Funct1n) Two kinds of . Among them, the hard threshold function can well preserve the detailed characteristics of the signal , But at the threshold ±T A discontinuity , And it is not differentiable , At the same time, it eliminates wavelet coefficients smaller than the threshold , Wavelet coefficients larger than the threshold are completely retained without processing , Therefore, the reconstructed signal is easy to produce a large mean square error , Oscillate ; Soft threshold function at threshold ±Τ The place is continuous , It can avoid the oscillation of the denoised signal , However, there is a constant deviation between the estimated wavelet coefficients and the wavelet coefficients of the actual signal , Make the reconstructed signal excessively smooth , Make the edges relatively blurred , It also affects the denoising effect .

Exponential soft and hard selection threshold noise reduction

Purpose ： Denoise the spectral signal , To reduce the noise residue of the spectral signal after noise reduction , The signal-to-noise ratio of spectral signal is improved .
Realization ：
step 1: Carry out multi-layer wavelet transform on the input noisy spectral signal . use db4 Wavelet transform is applied to noisy spectral signals 5 Layer decomposition , The low-frequency coefficients and high-frequency coefficients of wavelet are obtained respectively ;
step 2: For steps I The obtained high-frequency wavelet coefficients of each layer are shrunk . In the shrinkage processing, the threshold function adopts the exponential soft and hard selection threshold function proposed by the invention , namely

（Tj Threshold value ,ω jk For the first time j Wavelet coefficients of layers ,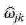 Is the wavelet coefficient after threshold shrinkage ,j Is the number of layers of wavelet decomposition ,k It means No k Wavelet coefficients .）
threshold Tj The hierarchical threshold is used to shrink the wavelet high-frequency coefficients of each layer , The layering threshold is 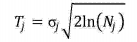Nj For wavelet decomposition j Length of layer wavelet coefficients , For the first time j Standard deviation of layer noise ,{ωjk} For the first time j Layer wavelet coefficients .
step 3: Wavelet inverse transform obtains wavelet LOCAL_LDLIBS += -lm

Denoised signal estimation . Use steps I The obtained wavelet low-frequency coefficients and steps 2 The high-frequency coefficients processed by wavelet threshold are transformed by wavelet inverse transform , Get the signal estimation value after wavelet layered denoising .
step 4: Signal median filter processing . In order to effectively remove the pulse interference in the noisy spectrum , For steps 3 The resulting signal estimate , Further carry out median filtering .

Compared with the traditional threshold function, the soft and hard threshold function of this index has the following advantages :
(1) When |ωjk|≥Tj when , The exponential soft and hard selection threshold function has a high-order derivative ;
(2) The asymptotic equation of the function is 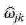=ωjk, It overcomes the problem estimated by simple soft threshold function 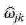With constant deviation Tj(|ωjk|≥Tj) Limitations , So we can better 、 Retain the peak point of spectral signal more completely .
Effect evaluation ：
SNR：

MSE：

Extend Empirical Mode Decomposition Extended empirical mode decomposition

The key of the method is empirical mode decomposition , It can decompose complex signals into finite eigenmode functions （Intrinsic Mode Function, abbreviation IMF）, Each decomposed IMF The component contains the local characteristic signals of different time scales of the original signal . Empirical mode decomposition method can stabilize non-stationary data , Then Hilbert transform is performed to obtain the time spectrum , Get a physically meaningful frequency .
EMD decomposition method
EMD Decompose the original signal into eigenmode functions (IMF) component
An eigenmode function is ：
⑴l Function in the whole time range , The number of local extreme points and zero crossings must be equal or at most one difference ;
⑵ At any point in time , Envelope of local maximum （ The upper envelope ） And the envelope of the local minimum （ The lower envelope ） The average must be zero .
EMD The decomposition process
a. The screening process is EMD It is used to decompose the signal into IMF The process of .
b. For a signal X(t), The upper and lower envelopes are determined from the local maximum and minimum values of cubic spline interpolation , Give Way m1 Represents the mean value of the upper and lower envelopes . Locality is determined by any parameter ; Calculate time and EMD The validity of depends largely on this parameter .
c. The first component h1 computing method ：h1=X(t)-m1
d. In the second screening process ,h1 Treated as data ,m11 yes h1 The mean value of the upper and lower envelopes of ：h11=h1-m11
e. The screening process is repeated k Time , until h1k Is an eigenmode function , namely ：h1(k-1)-m1k=h1k
f. Then it is designated c1=h1k, The first one in the data IMF component , It contains the shortest periodic component in the signal . We separate it from the rest of the data ：X(t)-c1 = r1 The process repeats rj Time ：r1-c2 = r2,…,rn-1 - cn = rn.
g. The result is a set of functions ; The number of functions in the set depends on the original signal .

EEMD characteristic
Inherited EMD Adaptability of ; White noise disturbance is introduced and set averaging , The problem of scale mixing is avoided , Make the final decomposition IMFs Maintain physical uniqueness .
EEMD Specific steps ：
1） Superimpose the white noise sequence with given amplitude on the data sequence to be analyzed .
2） The data after adding white noise —— Mixed signals ( The original signal ) Conduct EMD decompose .
3） Repeat these two steps repeatedly , Each time a new white noise sequence with the same amplitude is added, different IMFs.
4） Finally, it is obtained by decomposing each time IMFs Find the set average , And take it as the final decomposition result .
In this way, we get IMFs. Besides , EMD Except that there is no guarantee for everyone IMF Both have good physical meaning , Nor can we estimate the result of decomposition IMFs The reliability of . but EEMD The significance test can be carried out with the help of the set disturbance of white noise , So as to give each IMF The reliability of .

source ：
zhuanlan.zhihu.com/p/22450818
https://patents.google.com/patent/CN104182946A/
https://www.cnblogs.com/jiangleads/articles/9462087.html