Hello friend , The content of this blog involves the storage of plastic family in memory and floating-point family in memory , The plastic family includes char,short,int,long,longlong, The floating-point family contains float,double, The plastic family is divided into unsigned plastic and signed plastic , Because of the difference between positive and negative , Of course, the range of values is different , When you understand and practice , You will find it wonderful , You will be amazed at how different the bosses who discovered these computer storage methods are from ordinary people .

Catalog

1. Shaping storage in memory

( One ) Original code , Inverse code , The specific content of complement

( Two ) Why is the complement stored in memory ？

( 3、 ... and ) Introduction to big and small end

1. What is the big and small end ?

2. Why are there big and small ends ?

( Four )char Storage of type in memory

2. Floating point storage in memory

( One ) Examples of floating point storage

( Two ). Floating point storage rules

( 3、 ... and )E There are three situations when storing in memory

1.E Not all for 0 Or not all of them 1

2.E All for 0

3.E All for 1

1. Shaping storage in memory

( One ) Original code , Inverse code , The specific content of complement

There are three binary representations of integers in computers : Original code , Inverse code , Complement code .

1. Original code : Directly convert decimal to binary , for example :-15-----1000 0000 0000 0000 0000 0000 0000 1111

2. Inverse code : Except for the highest sign bit of the original code , Other bits press ( Binary system ) Bit inversion , Symbol bit 1, Decimal is negative , by 0 Then positive number

for example :-15 The original code of : 1000 0000 0000 0000 0000 0000 0000 1111

                 Inverse code :  1111 1111  1111  1111  1111  1111  1111  0000

3. A complement is a counter code +1:1111 1111 1111 1111 1111 1111 1111 0001

( The original and inverse complements of positive numbers are the same , The original inverse complement of negative numbers is different , What plastic stores in memory is a complement , Original code when printing )

( Two ) Why is the complement stored in memory ？

In computer system , All values are represented and stored by complements . The reason lies in , Use complement , You can combine sign bits and numeric fields One processing ; meanwhile , Addition and subtraction can also be handled in a unified way （CPU Only adders ） Besides , Complement code and original code are converted to each other , Its operation process It's the same , No need for additional hardware circuits .

Take a chestnut :

  Arithmetic conversion ( From bottom to top )

Then take a look at the following code , What is the answer printed ？

size_t And unsigned int The same is unsigned

#include <stdio.h>
int main()
{
	size_t a = 1;
	int b = 2;
	if (a - b >= 0)
		printf(" Greater than \n");
	else
		printf(" Less than \n");
	return 0;
}

Because as just said ,size_t a No sign ,b For the sign , There are differences between the two symbol types , When calculating, you need to calculate   in , therefore , Signed will be converted to unsigned , Unsigned minus unsigned is always greater than or equal to 0, So the printed answer is : Greater than .    

  Next I use VS The compiler shows you the storage of integer values in memory

Curious you will find , alas ？ Wrong! ! The complement in memory should not be 00 00 00 14 Do you , Should not be ff ff ff f6 Do you ？

So here is the content of the size side .

( 3、 ... and ) Introduction to big and small end

1. What is the big and small end ?

Big end （ Storage ） Pattern , The low bit of data is stored in the high address of memory , And the high end of the data , Low address saved in memory in ;

The small end （ Storage ） Pattern , The low bit of data is stored in the low address of memory , And the high end of the data ,, Stored in memory Address .

2. Why are there big and small ends ?

Why are there big and small end patterns ？ This is because in a computer system , We are in bytes , Each address unit Each corresponds to a byte , A byte is 8 bit. But in C In language, except 8 bit Of char outside , also 16 bit Of short type ,32 bit Of long type （ It depends on the compiler ）, in addition , For digits greater than 8 Bit processor , for example 16 Bits or 32 Bit processor , Because the register width is larger than one byte , So there must be a problem of how to arrange multiple bytes . because This leads to the big end storage mode and the small end storage mode , Store in byte order .

for example ： One 16bit Of short type x , The address in memory is 0x0010 , x The value of is 0x1122 , that 0x11 by High byte , 0x22 Is low byte . For big end mode , will 0x11 Put it in the low address , namely 0x0010 in , 0x22 Put it high In the address , namely 0x0011 in , In the memory above , The left is low and the right is high , Is shown as 2211. The small end model , Just the opposite . That we use a lot X86 The structure is small end mode , and KEIL C51 be For big end mode . A great deal of ARM,DSP It's all small end mode . There are some ARM The processor can also The hardware chooses the big end mode Or small end mode .

Baidu 2015 System Engineer written test questions ：

Please briefly describe the concepts of big end byte order and small end byte order , Design a small program to determine the current machine byte order .（10 branch ）

include <stdio.h>
int check_sys()
{
 int i = 1;
 return (*(char *)&i);
}
int main()
{
 int ret = check_sys();
 if(ret == 1)
 {
 printf(" The small end \n");
 }
 else
 {
 printf(" Big end \n");
 }
 return 0;
}

The answer here is to print the small end ,1 Of 16 Into the system for 0x00 00 00 01 Take the address and forcibly convert it to char* Pointer dereference access char The returned value of byte size of type is 1, So the low order is displayed in memory -> The high position should be 01 00 00 00 Small end storage , If the memory shows 00 00 00 01 Big end storage , The return value is 0, Be careful : Here, two numbers in hexadecimal are a pair , namely 1 The size of bytes , Pointers of the same size can be stored with each other , The amount of bytes accessed when dereferencing is determined by the family type .

( Four )char Storage of type in memory

A signed char Value range of :-128~127  Unsigned char Value range of :0~255

Practice it , What's the result of the print ?

#include <stdio.h>
int main()
{
	char a = -128;
	printf("%u\n", a);
	return 0;
}

Explain ：-128 The binary of is 10000000 00000000 00000000 10000000, Put it in char Truncation occurred in type ,a Can only store 1 Bytes , therefore a The binary of is 10000000, Be careful ：int The default type is unsigned int, however char The default signed or unsigned type of type depends on the compiler . The binary 127 by 01111111,10000000 by 128, The high bit is the sign bit , So remember to have symbols char in 1 And seven 0 The binary system is -128, The printing form is unsigned int type , So we need to improve , High complement sign bit , Binary for :11111111111111111111111110000000, The original and inverse complements of positive numbers are the same , Convert binary to decimal and print as 4294967168.

  Take a look at the second question :

#include <stdio.h>
int main()
{
    int i= -20;
    unsigned  int  j = 10;
    printf("%d\n", i+j);
    return 0;
}

This problem exists Arithmetic conversion Signed and unsigned addition , Signed is converted to unsigned .

  Third question , Combine theory with practice :

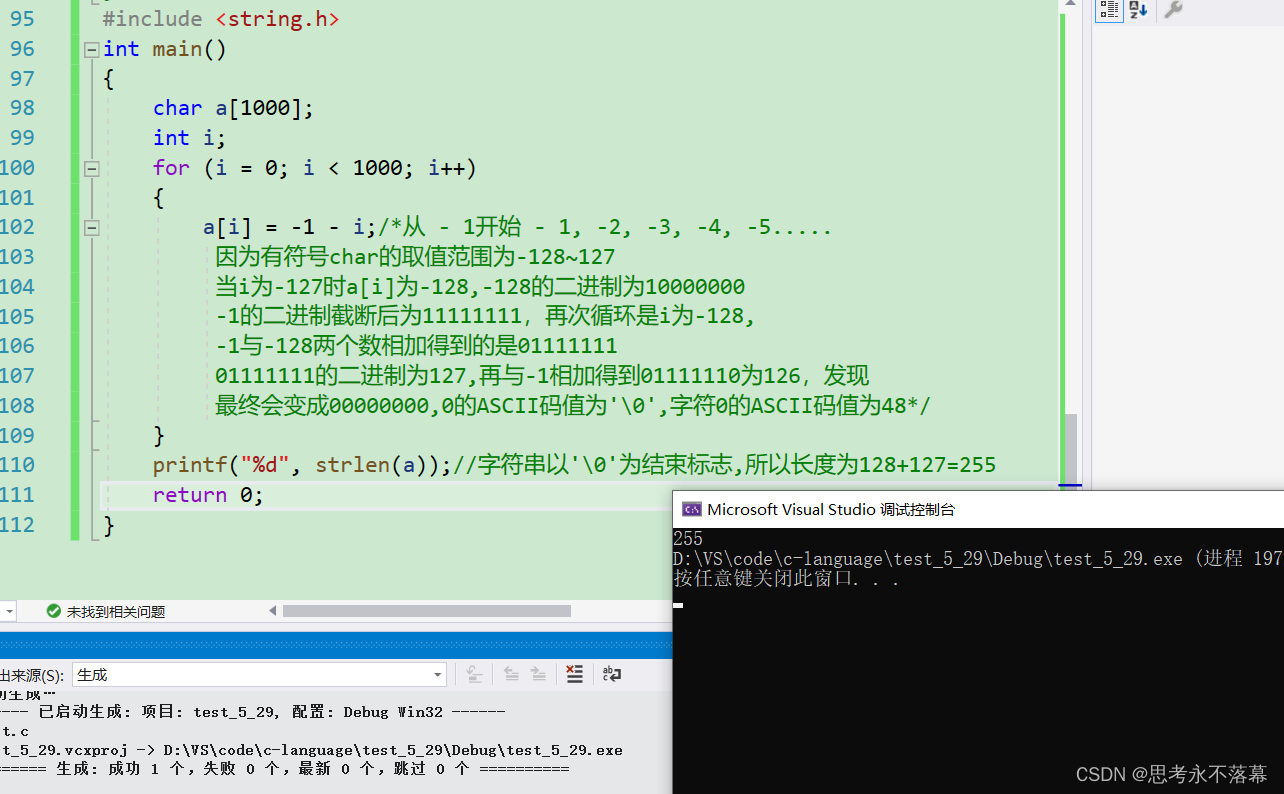
#include <stdio.h>
#include <string.h>
int main()
{
    char a[1000];
    int i;
    for(i=0; i<1000; i++)
   {
        a[i] = -1-i;
   }
    printf("%d",strlen(a));
    return 0;
}

2. Floating point storage in memory

 ( One ) Examples of floating point storage

#include <stdio.h>
int main()
{
 int n = 9;
 float *pFloat = (float *)&n;
 printf("n The value of is ：%d\n",n);
 printf("*pFloat The value of is ：%f\n",*pFloat);
 *pFloat = 9.0;
 printf("num The value of is ：%d\n",n);
 printf("*pFloat The value of is ：%f\n",*pFloat);
 return 0;
}

Output result :

( Two ). Floating point storage rules

According to international standards IEEE（ Institute of electrical and Electronic Engineering ） 754, Any binary floating point number V It can be expressed in the following form ： (-1)^S * M * 2^E ,(-1)^S The sign bit , When S=0,V Is a positive number ; When S=1,V It's a negative number . M Represents a significant number , Greater than or equal to 1, Less than 2. 2^E Indicates the index bit .

for instance ： Decimal 9.0, Written as binary is 1001.0 , amount to 1.001×2^3 . that , According to the above V The format of , We can draw S=0,M=1.001,E=3. Decimal -5.0, Written as binary is -101.0 , amount to -1.01×2^2 . that ,S=1,M=1.01,E=2.

Then you may ask , Some decimals can't be saved accurately ？

Yes , for example 9.6f

  decimal The power of the bit after the dot is negative , for example 0.1 Medium 1 yes 1*2^-1 namely 0.5, Find it later 0.25,0.125,0.0625 We found that Can't save accurately Of , We need to know .

IEEE 754 Regulations ： about 32 Floating point number of bits , The highest 1 Bits are sign bits s, And then 8 Bits are exponents E, The rest 23 Bits are significant numbers M.

  about 64 Floating point number of bits , The highest 1 Bits are sign bits S, And then 11 Bits are exponents E, The rest 52 Bits are significant numbers M.

  Keep it in the computer M when , By default, the first digit of this number is always 1, So it can be discarded , Save only the following decimal point . For example preservation 1.01 When the Hou , Save only 01, Wait until you read , Put the first 1 Add . The purpose of this , yes save 1 Significant digits , A more accurate one . for example 32 position , Leave to M 23 position , Omit 1 after , Leave to M Of 23 One more significant digit in the digit .

about E Come on ,E by unsigned int type , If E by 8 position , Its value range is 0~255; If E by 11 position , Its value range is 0~2047. however , We know , Scientific enumeration ( For example, let's give a 0.5,0.5 The binary of is 0.1(1*2^-1), therefore S=0,E=-1,N=1.0) Medium E You can have negative numbers ,EEE 754 Regulations , In memory E The true value of must be added with an intermediate number , about 8 Bit E, This middle number yes 127; about 11 Bit E, In the middle The number is 1023. such as ,2^10 Of E yes 10, So save it as 32 When floating-point numbers are in place , Must be saved as 10+127=137, namely 10001001.

( 3、 ... and )E There are three situations when storing in memory

1.E Not all for 0 Or not all of them 1

Index E The calculated value of minus 127（ or 1023）, Get the real value , And then the significant number M Add the first 1.

such as ： 0.5（1/2） The binary form of is 0.1, Since it is stipulated that the positive part must be 1, That is to move the decimal point to the right 1 position , Then for 1.0*2^(-1), Its order code is -1+127=126, Expressed as 01111110, And the mantissa 1.0 Remove the integer part and make it 0, A filling 0 To 23 position 00000000000000000000000, Then the second goes The system is expressed as :0 01111110 00000000000000000000000

2.E All for 0

E The original value was zero 1-127( or 1023), Significant figures are not added 1, And revert to 0.xxxxx Decimals of , Close to the 0 A very small number of , All indexes are 0, The significant number is original 1 Directly into 0

3.E All for 1

If all the significant figures are 0, Represents a large number , Positive and negative infinity , It depends on the sign bit S

Back to the first question ：

  Thank you for reading , If it helps you, please like , Comment or forward , Share with more in IT Programmers who forge ahead technically , Let's make progress together !